Premières définitions

Si H1 est l'hypertexte (U1, C1, d1, d1*) et H2 est (U2, C2, d2, d2*),

H1 H2 signifie qu'on a les inclusions correspondantes au niveau des ensembles d'unités d'information et des concepts, et que les restrictions de d2 et d2* à ces sous-ensembles sont équivalentes à d1 et d1* respectivement. Dit autrement: D1 D2 et D1* D2*.

On notera qu'il peut y avoir égalité des ensembles sans identité sur les hypertextes, ni même inclusion (si les relations sont incompatibles).

Si H1 et H2 et sont deux hypertextes faisant partie d'un domaine, on définira de manière évidente l'intersection et la réunion de ces hypertextes (par l'intersection et la réunion des ensembles de base et des ensembles liés aux relations).

Si H1 et H2 dans un domaine commun sont tels que :

D1 D2 = et D1* D2* =

on note leur réunion par H = H1H2 (somme directe).

Deux cas particuliers peuvent intervenir dans la construction d'un hypertexte: deux hypertextes sont dits juxtaposés s'ils n'ont pas d'unités d'information communes. Notation: H = H1_j H2.

En général on demande par contre qu'un lien existe entre H1 et H2, c'est-à-dire il existe c dans C1 C2 tel que du(u₁,c,u₂) avec u_i dans Ui (notion d'adjacence définie dans [LUC 96]). Dans ce cas on supposera souvent que C1 = C2 en prolongeant d et d* de façon triviale.

Par ailleurs deux hypertextes sont dits superposés s'ils n'ont pas de concepts communs. Notation: H = H1_s H2.

Dans ce cas on supposera souvent que U1 = U2 en prolongeant d et d* de façon triviale.

Les figures 4 et 5 présentent un cas simple de superposition. Les figures 6 et 7 illustrent les graphes dérivés.

	Figure 4: Représentation schématique d'un hypertexte H d'unités d'information u0, u1, u2, de concepts c1, c2, x1, x2.
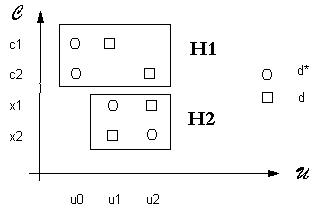	Figure 5: Graphe des relations d et d* de H avec la représentation de H comme superposition de H1 et H2.
	Figure 6: Graphe de la relation dérivée entre les unités d'information pour H1, H2 et H.
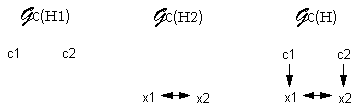	Figure 7: Graphe de la relation dérivée entre les concepts pour H1, H2 et H. On notera, la perte d'information à ce niveau occasionnée lors de la décomposition.

Un exemple de juxtaposition est donné par l'ajout d'une fiche dans une base de donnée.

Représentation matricielle

Du point de vue matricielle, la juxtaposition revient à mettre côte à côte les matrices représentant les relations d et d*. La superposition revient à mettre l'une sur l'autre les matrices représentant les relaitons d et d*.

Transformation des coefficients par somme directe

On suppose H = H1H2. On notera à l'aide d'un indice les coefficients liés à H1 et H2.

Les coefficients de la somme sont en général la somme des coefficients ou des moyennes pondérées de ces coefficients. Cela donne une nouvelle famille de relations (II):

II.1: N = N₁ + N₂ ; N* = N*₁ + N*₂ ; avec

#U = #U₁ + #U₂ (juxtaposition) ;

#C = #C₁ + #C₂ (superposition)

II.2: Re(c) = Re₁(c) + Re₂(c) ; Re*(c) = Re₁*(c) + Re₂*(c)

Dans le cas de la superposition un des deux termes de la somme est nul, en admettant une extension triviale de d et d* aux concepts non définis dans un des hypertextes.

II.3: Di(u) = Di₁(u) + Di₂(u) ; Di*(u) = Di₁*(u) + Di₂*(u)

Dans le cas de la juxtaposition un des deux termes de la somme est nul.

II.4: Rr(c) = (Re₁(c) + Re₂(c)) / N =
Rr₁(c) (N₁/N) + Rr₂(c) (N₂/N) (idem pour Rr*(c))

II.5: Dr(u) = (Di₁(u) + Di₂(u)) / N =
Dr₁(u) (N₁/N) + Dr₂(u) (N₂/N) (idem pour Dr*(u))

II.6: Rm = Rm₁ (#C₁/#C) + Rm₂ (#C₂/#C) (idem pour Rm*)

Avec #C_i/#C = 1 dans le cas d'une superposition avec égalité des ensembles d'unités d'information.

II.7: Dm = Dm₁ (#U₁/#U) + Dm₂ (#U₂/#U) (idem pour Dm*)

Avec #U_i/#U = 1 dans le cas d'une juxtaposition avec égalité des ensembles de concepts

II.8: E(u) = Di*(u)/Di(u) = (Di₁*(u) + Di₂*(u))/Di(u)

donc E(u) = E₁(u) (Di₁(u)/Di(u)) + E₂(u) (Di₂(u)/Di(u))

II.9: de même: C(c) = C₁(c) (Re₁(c)/Re(c)) + C₂(u) (Re₂(c)/Re(c))

Il n'existe évidemment pas de relations simples pour les coefficients dérivés. En considérant par exemple ceux concernant les unités d'information dans le cas d'une juxtaposition, les valeurs des VX1(u) dans l'hypertexe H1 supposé contenir u, seront d'autant plus proche de VX(u) que u sera déconnectée de H2. Cette remarque s'avére utile lorsqu'il s'agit de décomposer un hypertexte de façon à perdre le moins d'information possible.

Le tableau 4 reprend le cas de la base de données et de l'arborescence avec ajout d'une fiche ou d'un champ dans le cas de la base de fiches, et d'un niveau dans le cas de l'arborescence. Il montre différents types de fonction d'évolution des coefficients, linéaire, en 1/x ou exponentiel (de base inférieure ou supérieure à 1).

Tableau 4: L'évolution des coefficient par rajout d'une unité d'information.

	#U	#C	N	N*
Rajout d'une fiche	n -> n+1	p	np -> np+p	0
Rajout d'un champ	n	p -> p+1	np -> np+n	0
Rajout d'un niveau (->+1)	n -> n + +1	p -> p + +1	p -> p + +1	p -> p + +1

	Re(c)	Re*(c)	Di(u)	Di*(u)
Rajout d'une fiche	n -> n+1	0	p	0
Rajout d'un champ	n	0	p -> p+1	0
Rajout d'un niveau (->+1)	1	1	0, 1	, 0

	Rr(c)	Rr*(c)	Dr(u)	Dr*(u)
Rajout d'une fiche	1/p	indéfini	1/n -> 1/(n+1)	indéfini
Rajout d'un champ	1/p -> 1/(p+1)	indéfini	1/n	indéfini
Rajout d'un niveau (->+1)	1/p -> 1/(p + +1)	1/p -> 1/(p + +1)	0, 1/p -> 1/(p + +1)	/p -> /(p + +1), 0

	Rm	Rm*	Dm	Dm*
Rajout d'une fiche	n -> n+1	0	p	0
Rajout d'un champ	n	0	p -> p+1	0
Rajout d'un niveau (->+1)	1	1	->1	->

	E(u)	C(c)
Rajout d'une fiche	0	0
Rajout d'un champ	0	0
Rajout d'un niveau(->+1)	, , 1	1