Position du problème

Le but de ce document est de comparer les coefficients "classiques" [1] construits à partir de la matrice des distances avec les coeffcients obtenus à partir de la "matrice de circulation" (S) introduite dans le document structure d'un hypertexte sous forme matricielle. Les exemples qui seront utilisés sont repris du même document. Ils sont donnés dans les figures 1 et 2.

Les coefficients de structure classiques sont calculés à partir de la matrice des distances converties D = [d_ij] où d_ij est le plus court chemin entre les sommets i et j et un "grand" nombre, K (constante de conversion, souvent  K vaut le nombre de noeuds), s'il n'y a pas de chemin du sommet i au sommet j. Ils seront rappelés sur la base d'un exemple.  

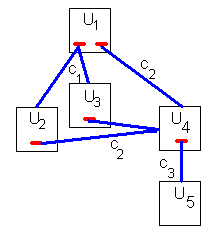
Figure 1: un hypertexte constitué de cinq unités d'information et de trois concepts.

Pour l'hypertexte donné dans la figure 1, la matrice initiale des distances est :

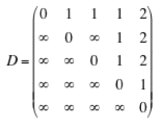
En remplaçant les coeffcients infinis par 10 (2 fois le nombre de sommets), on obtient la matrice des distances convertie.

Centralité relative

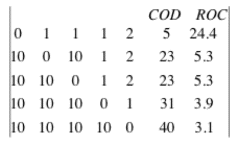
La somme des coefficient de la ligne i est la distance de sortie convertie du noeud i (converted out distance - COD_i). On définit la centralité relative de sortie (relative out centrality - ROC_i) par ROC_i = CD / COD_i où CD est la somme de toutes les distance (dans l'exemple CD =  122).

De même la somme des coefficient de la colonne j est la distance d'entrée convertie du noeud j (converted in distance - CID_j). On définit la centralité relative d'entrée (relative in centrality - RIC_j) par RIC_j = CD / CID_j .

Plus ROC est grand (COD est petit), et plus le noeud est une "racine". Classiquement, un index est un noeud dont l'indice ROC est supérieur à la moyenne augmentée de 3 écarts type. De façon duale, les noeuds de référence sont ceux dont la valeur RIC est grande.

Nous voulons comparer les coefficients ROC et RIC avec les valeurs calculées à partir de notre matrice de structure, ou matrice de "circulation" (matrice de la complétion transitive pondérée du graphe) qui vaut [2]:

Les sommes des lignes sont respectivement (sans la diagonale) [3]:  (0.81, 0.75, 0.75, 0.5, 0), à comparer avec  ROC. Les sommes des colonnes sont respectivement (sans la diagonale) :  (0, 0.13, 0.13, 1.37, 1.19), à comparer avec  RIC.

Par rapport aux coefficients classiques, on note que:

• Les ordres de grandeur sont différents, l'échelle est moins contrastée. Mais les contrastes observés dans le cas classique dépendent de la valeur de K.
  
• L'ordonnancement des noeuds en tant que racine est le même (la première unité d'information est un index).
• L'ordonnancement des noeuds en tant que référence varie. La meilleure référence est l'unité 5 avec les coefficients standard et l'unité 4 avec les autres coefficients.
  

On notera encore dans notre cas, que les valeurs ne dépendent pas seulement du graphe final, mais aussi de la structure "descripteur-référent" qui lui donne naissance.

Exemple 2

Un autre exemple est encore fourni par celui de la figure 2.

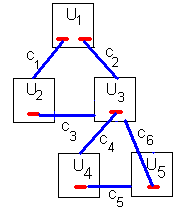
Figure 2: un hypertexte constitué de cinq unités d'information et de six concepts avec une "boucle".

On calcule les coeffcients avec K=10.

A comparer les valeurs de ROC et RIC avec les valeurs données par la matrice de circulation (S-diag(S)), respectivement (1, 1, 0.857, 0.857, 0.897) et (0, 0.25, 1.857, 1.357, 1.107).

Ce dernier exemple montre bien la particularité de la matrice de circulation. Les deux premiers noeuds ont une même valeur maximum de sortie [3]. Cela ne contredit pas le fait que ces deux noeuds sont relativement centraux. De ce point de vue la version classique est plus précise.

La compacité

La compacité est donnée de façon standard par (Max - sd) / (Max - Min) avec :

• Max = K(N² - N) (graphe à N noeuds sans liens)
• Min = N² - N (graphe complet à N noeuds)
• sd = somme des coefficients de la matrice des distances convertie.

Il est possible de créer les deux hypertextes extrêmes  dans le modèle "document x concept".  Le cas Max est donné par l'absence de concept. La matrice S associée est l'dentité et la somme correspondante est nulle (c'est donc un minimum noté Smin). Le cas Min  est donné par la présence de tous les concepts (en nombre k = nombre de noeuds) comme descripteur et référent de chaque noeud (unité d'information). Les matrices  D (descripteurs) et R (référents) valent U. La matrice associée du graphe est donc kU où U est la matrice dont tous les coefficients valent 1. Les matrices  pondérées des descripteurs et des référents valent U/k. Donc:

S = 1 + (1/2k)U + (1/2k)²U² + (1/2k)³U³ + ...

Mais U² = k U . Donc:

S = 1 + (1/2k)U + (1/2k)²kU + (1/2k)³k²U + ...

S = 1 + U ( (1/2k) + (1/2)²(1/k) + (1/2)³ (1/k) + (1/2)⁴ (1/k) + ...)

S = 1 + U/k ( (1/2) + (1/2)² + (1/2)³ + ...) = 1 + U/k

Smax est la somme des coefficients de S-disg(S). On trouve:

 Smax = k² / k = k

Partant d'un graphe complet, ce résultat aurait pu être déduit directement. Le coeffcient de compacité donné par la matrice de circulation est:

sc/Smax

Il vaut également 0 dans le cas d'un hypertexte totalement deconnecté et 1 dans le cas de l'hypertexte complet.

Le calcul pour les exemples 1 et 2 sont les suivants:

Cas standard

exemple	K = N (nb de noeuds)	Min	Max	sd	compacité
1	5	20	100	67	33/80 (0.41)
2	5	20	100	57	43/80 (0.54)

Avec la matrice de circulation

exemple	K (nb de noeuds)	Smax	sc	compacité
1	5	5	2.81	0.562
2	5	5	4.57	0.914

Les informations sont comparables. A noter que dans le cas de l'hypertexte donné par les référents et descripteurs, plusieurs hypertextes différents peuvent conduire à un graphe réduit identique. Il y a aussi plus d'une façon de réaliser un hypertexte dont le graphe associé est un graphe complet.

Une autre alternative au coefficient de compacité standard [3] pourrait être obtenue en utilisant les valeurs propres.

Stratification

Ce coefficient capture le degré de linéarité de l'hypertexte. De façon classique, on définit pour un noeud: le statut (nombre de liens en sortie), le contrestatut (nombre de liens en entrée). Le prestige est alors la différence (statut - contrestatut).

On définit pour un hypertexte: le prestige absolu (somme des valeurs absolues du prestige de chaque noeud). On définit également le "linear absolute prestige - LAP" qui est le prestige absolu d'un hypertexte linénaire avec  N noeuds)

La stratification (stratum) est le rapport du prestige absolu au LAP.

On peut suivre le même algorithme pour la matrice de circulation, en sachant également que plusieurs hypertextes peuvent conduire au même graphe associé. De même, il n'y a pas qu'un seul hypertexte "linéaire" de référence.

On prend dans ce cas pour l'hypertexte linéaire la matrice R valant 1 dans la "diagonale". Quant-à D, il s'agit de la matrice avec des 1 dans la sous-diagonale.

Un hypertexte linéaire a donc pour graphe:

Calcul du LAP: cas standard, N = 5

La matrice des distances est:

LAP = (10-0) + (6-1) + (3-3) + abs(1-6) + abs(0-10) = 30

Calcul du LAP, matrice de circulation N=5

Les matrices R et D sont:

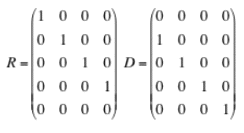
La matrice pondérée du graphe G est la matrice de dimension 5 x 5 nulle avec des 1 dans la sur-diagonales. Cela donne pour S:

LAP = (15/16-0) + (7/8-1/2) + (3/4-3/4) + abs(1/2-7/8) + abs(0-15/16)
LAP =  15/8 + 3/4 = 21/8

Le calcul pour les exemples 1 et 2 sont les suivants:

Cas standard

exemple	N (nb de noeuds)	LAP	prestige abs.	stratum
1	5	30	18	0.6
2	5	30	24	0.8

Avec la matrice de circulation

exemple	N (nb de noeuds)	LAP	prestige abs.	stratum
1	5	21/8	4.1	0.64
2	5	21/8	3.5	0.75

Dans le cas standard, un hypertexte linéaire possède un "stratum" de 1. Cette valeur est maximale.  S'il est possible d'atteindre n'importe quel noeud à partir de n'importe quel noeud, le stratum est nulle.

Dans notre cas, la valeur du LAP est minimum. Ce qui conduit à définir le stratum comme LAP / prestige absolu.

Pour conclure

En définitive, des indices métriques de centralité, compacités et stratum peuvent être obtenus à partir de la matrice de circulation. Ils semblent donner, à quelques nuances près, des informations comparables à celles obtenues par les coefficients calculés classiquement à partir de la matrice des distances. Cette hypothèse resterait à tester avec d'autres exemples. Notamment pour explorer les "nuances" constatées et pour explorer l'effet de la structure sous-jacente (descripteur - référent) sur ces coefficients.

---

1) Botafogo, R.A., Revlin, E. & Schneiderman, B. (1992). Structural Analysis of Hypertexts: Identifying hierarchies and Useful Metrics. ACM Transactions on Information Sytems, 10 (2), 142-180.

2) La matrice de circulation est une matrice "d'anti-distance". Pour des raisons de signification ultérieure, on ne considère pas la diagonale. D'autres façon de faire sont possibles, notamment avec l'utilisation de la diagonale et l'ajout d'une pondération (somme des coefficients).

3) De fait on utilise S-diag(S). Bref rappel de la signification de S: le coefficient s_ij est la probabilité de passer de l'unité i à l'unité j avec la convention suivante: on part de l'unité i, on choisit un référent (équiprobabilité). Si ce référent peut conduire à plusieurs unités, on en choisit une (équiprobabilité). De là on décide ou pas de repartir avec une probabilité de 1/2. Avec cette définition, on peut s'étonner que la somme d'une ligne de S-1 ne soit pas égale à 1. Cela est dû au fait que les choix sont liés aux concepts servant de lien (le choix est fait en tenant compte de l'ensemble des unités où le concept est référent et/ou descripteur). Ainsi les décisions prises à chaque étape ne sont pas totalement indépendantes. Dans le deuxième exemple chaque lien est lié à un concept particulier. Dans ce cas, il y a indépendance des décisions et la somme des lignes vérifie la propriété d'être égale à 1.  

Par ailleurs, deux hypertextes qui présenteraient au niveau du graphe associé exactement les mêmes liens, peuvent conduire à des matrices de circulation différentes. Celles-ci sont dépendantes des concepts qui ont donné lieu aux liens.