Introduction

Dans ce document, il est rendu compte de la structure du graphe associé à des hypertextes construits à partir des deux relations "descripteur" et "référents" [1]. Les manipulations effectuées sont décrites selon la syntaxe de Matlab. Des documents complémentaires sont disponibles dans l'archive simu2-htxt.zip.

Pour comparaison, on signale la procédure de construction par degré attirance (ou par agrégation) décrite dans [3] qui produit des graphes "scale free" (graphe de nature fractale) avec une distribution des liens suivant une loi puissance (de type x^-n n fixe) [4], procédé qui rend compte de la façon dont le web se construit.

Dans ce document, on commence par faire quelques hypothèses théoriques suivies de simulations et de recherche de structure selon les procédés décrits dans [5].

Hypothèses

L'hypothèse principale est que le nombre de descripteurs et les descripteurs eux-mêmes sont attribués au hasard (de façon uniforme) à l'intérieur de chaque unité d'information. Et qu'il en va de même pour les référents. A ce procédé répond donc un graphe "isotrope". C'est-à-dire que la probabilité qu'un lien existe entre deux sommets x et y est une constante.

Cette propriété d'isotropie entraîne que la répartition des Ui en fonction du nombre de liens "rentrants" ou "sortants" suit une loi binomiale (annexe 1).

Il est évident que le paramètre de ces distributions va dépendre de la densité des descripteurs et référents pour chaque Ui. Par contre, la façon dont cette densité intervient est plus difficile à estimer. L'annexe 2 en propose une estimation.

On peut également prévoir que ces hypertextes vont possèder un assez haut degré de connectivité.

Il est également prévisible que des quasi-composantes connexes vont faire leur apparition si la distribution des concepts dans les unités d'informations ne se fait plus de façon de façon uniforme (c'est-à-dire si certains concepts ont des liens privilégiés avec certaines Ui). L'influence de cette distribution sur la connectivité de l'hypertexte est également difficile à prévoir. Une étude expérimentale est faire à ce propos dans un autres documents.

Les exemples à distribution uniforme

Trois exemples sont traités qui suivent la même procédure. Il varient par le nombre total de concepts et le nombre maximum de descripteurs / référents par Ui. Les manipulations pour décrire la structure sont décrite dans [5].

Exemple 1000 - 100 (10, 20)

Le premier hypertexte généré contient 1000 documents et 100 concepts avec au maximum 10 descripteurs et 20 référents par document. Le nombre de descripteurs et de référents associes à une Ui est pris au hasard selon une distribution uniforme.

Concrètement la matrice des descripteurs D et celle des référents sont créées par:

D = new_docXmot(1000,100,10)

R = new_docXmot(1000,100,20)

La matrice du graphe est donnée par : G = R*D'. Puis le graphe est rendu univalué (G = G&G).

Dans le cas particulier, le graphe obtenu a 1000 sommets et 361014 arêtes. Les figures 3 et 4 montrent la distribution des liens "sur" et "à partir de" (techniquement rendu par hist(sum(G,1)) et hist(sum(G,2)).

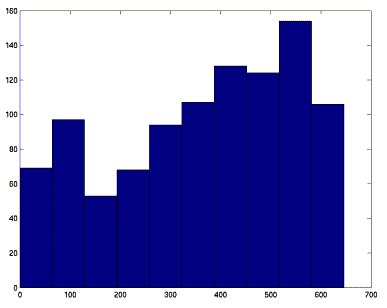
fig 3. Distribution du nombre de liens sur les Ui

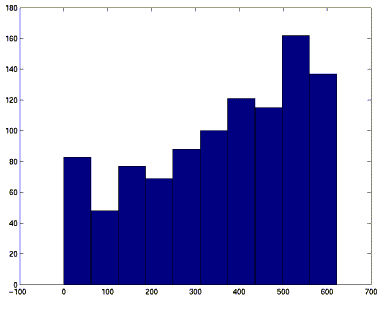
fig 4. Distribution du nombre de liens à partir des Ui

L'annexe 1 montre que ces distributions suivent une loi binomiale. L'annexe 2 en estime les paramètres.

Connexité du graphe non orienté

On symétrise et univalue G (Gx = G+G', puis par Gx&Gx).

En cherchant la multiplicité de la valeur propre 0 du laplacien combinatoire (diag(sum(Gx,2)) - Gx) on obtient le nombre de composantes connexes. En l'occurence ce nombre est 2. L'examen du vecteur propre correspondant montre qu'un des composantes se réduit à une unité d'information (u994).

La première valeur propre non nulle est 40 ce qui est l'indice d'une connectivité élevée pour les 999 sommets restants (il faut ôter au moins 40 sommets pour décomposer le graphe en deux composantes).

Autorités et hubs

La recherche des valeurs propres de GG1 = G*G' donne comme valeur maximum 201130. Le vecteur associé à cette valeur maximum (dans ss1.txt) a (environ) 40 composantes nulles (puits). Les autres composantes varient entre 0.0031824 et 0.047603. Sans vraiment mettre en évidence des hubs, ce qui correspond bien à la figure 4.

Le même travail avec G1G = G'*G conduit à un vecteur propre associé (dans s1s.txt) avec 69 valeurs nulles (sources). Les autres composantes varient entre 0.0066216 et 0.049631.

Structure papillon

Le but est de chercher le CORE de l'hypertexte construit. La procédure est la suivante:

1. recherche de la fermeture transitive GB =G * (I-G/(||G||+1))^(-1);
2. univaluation: GB = GB & GB;
3. recherche pour chaque Ui du nombre d'unités (t(i)) qui peuvent être atteintes et qui peuvent l'atteindre. t(i) = sum(GB(i,:)&GB(:,i))

Le maximum obtenu est 960, donc t(i) = 960 pour 960 Ui [7]. Les 40 Ui restantes ne génèrent qu'un CORE trivial (réduit à elle-même). De façon détaillée:

• 4 Ui ne peuvent attendre aucune Ui (autre qu'elle-même)
• Les autres peuvent en atteindre 963 ou 962
• 37 Ui ne peuvent être atteintes (sauf par elle-même)
• Les autres peuvent être atteintes de 996 autres (ou parfois 995 ou 997)
• L'Ui 994 est isolée

Remarques

On constate aisément que les hypothèses sont vérifiées. Toutefois, il est à remarquer que un nombres important d'Ui ont plus de 500 liens entrants ou sortants. A noter également, la grande connectivité du graphe et le CORE constitué de 96% des Ui.

Exemple 1000 - 1000 (10-20)

Le deuxième exemple traité va contenir 1000 documents et 1000 concepts avec au maximum 10 descripteurs et 20 référents par document. L'hypertexte est obtenu selon la même procédure que précéendemment. Le graphe associé contient 1000 sommets et 44768 arêtes

Les distributions des descripteurs et référents sont donnés dans les figures 5 et 6.

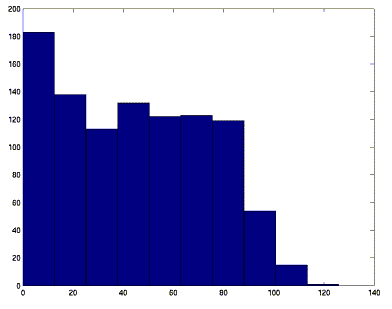
fig 5. Distribution du nombre de liens sur des Ui

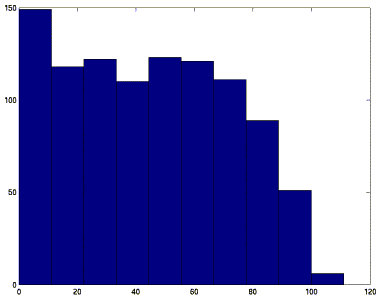
fig 6. Distribution du nombre de liens à partir des Ui

• 17 Ui ne peuvent attendre aucune Ui (autre qu'elle-même)
• 54 Ui ne peuvent être atteintes (sauf par elle-même)
• 5 Ui sont isolées

Remarque

Par rapport au cas précédent on note la forte diminution du maximum de liens entrants/sortants (moins de 10 Ui ont plus de 100 de ces liens). La connectivité a également fortement diminué mais le CORE est encore constitué de 93% des Ui.

Exemple 1000 - 1000 (5, 10)

Le dernier exemple traité va également contenir 1000 documents et 1000 concepts avec au maximum 5 descripteurs et 10 référents par document. L'hypertexte est obtenu selon la même procédure que précédemment. Le graphe associé contient 1000 sommets et 11682 arêtes

Les distributions des descripteurs et référents sont donnés dans les figures 7 et 8.

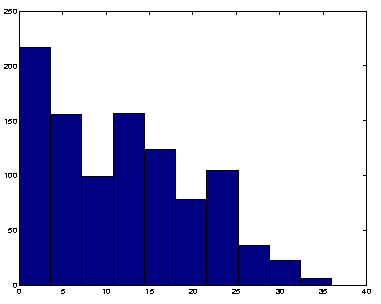
fig 7. Distribution du nombre de liens sur des Ui

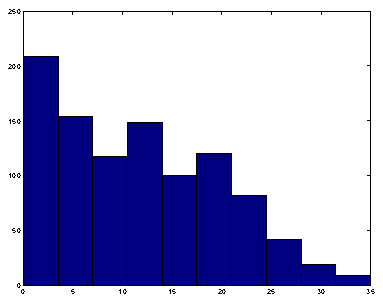
fig 8. Distribution du nombre de liens à partir des Ui

Notes

[1] Voir le document: Définition formelle d'un hypertexte et calcul de coefficients locaux.

[2] Barabasi, A.-L. (2002). Linked, The New Science of Networks. Cambridge, MA : Perseus Publishing.

[3] Un simulateur pour la création d'hypertextes.

[4] Quelle équivalence entre ces deux caractéristiques ? Trois structures principales sont proposées pour les réseaux: centralisée (l'étoile), décentralisée (hiérarchie d'étoiles), distribuée. A noter que Internet conçu selon l'architecture distribuée a évolué vers une structure décentralisée.

[5] Voir documents: Quelques manipulations pour déterminer la structure d'un hypertexte et Etude expérimentale de la structure d'un hypertexte obtenu par agrégation.

[6] Pour 6 unités d'information on obtient la valeur de 959, ce qui est impossible (les deux "CORES" auraient une Ui en commun et donc sont égaux). Ce résultat est dû au problème de l'identification de très petites valeurs à la valeur 0.

Annexe 1: distribution théorique du nombre de liens sur une Ui pour les hypertextes créés à partir des relations documents-concepts

Si n est le nombre d'unités d'information et si représente la probabilité qu'un lien existe entre 2 unités d'information données, la probabilité d'avoir x lien(s) sur une Ui est donnée par:

Annexe 2: calcul du paramètre de distribution théorique du nombre de liens sur une Ui pour les hypertextes créés à partir des relations documents-concepts

Notation :

Valeur de alpha

Par le fait que les liens sont univalués, on peut calculer = 1-' où ' est la probabilité que les concepts descripteur de la cibles soient différents des référents de la source.

Pour effectuer ce calcul, décompte les liens en série par le nombre de descripteurs de l'Ui cible. En appelant P(i) la probabilité d'avoir des concepts différents (de 0 à k) de i concepts donnés (variant de 0 à m) on a:

0 descripteur

Ce cas se présente avec la probabilité 1/(k+1). La probabilité de trouver une source avec référents différents est 1 :

1 descripteur

Ce cas se présente avec la probabilité 1/(k+1), il y a k cas possibles, chacun avec la probabilité 1/k.

La probabilité de trouver une source avec des référents différents vaut probabilité de prendre de 0 à m concepts parmi c, différents de celui du descripteur :

2 descripteurs

Ce cas se présente avec la probabilité 1/(k+1), il y a cas possibles, chacun avec la probabilité 1/.

La probabilité de trouver une source avec des référents différents vaut probabilité de prendre de 1 à m concepts parmi c, différents des deux descripteurs :

k descripteurs

Ce cas se présente avec la probabilité 1/(k+1), il y a cas possibles, chacun avec la probabilité 1/.

La probabilité de trouver une source avec des référents différents vaut probabilité de prendre de 1 à m concepts parmi c, différents des k descripteurs :

En sommant le tout, on a:

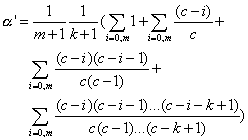
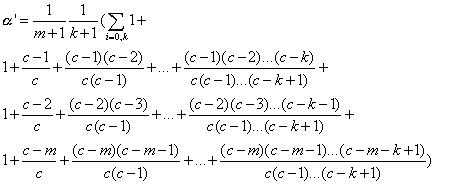
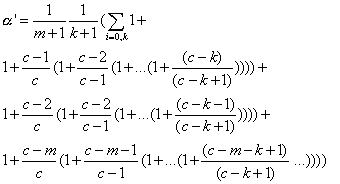
On trouve pour valeurs de ' resp. 0.648, 0.952, 0.988 pour les trois simulations. Donc vaut respectivement 0.352, 0.048, 0.018 ce qui conduit à des moyennes (n) de resp. 352, 48 et 18 ce qui correspond aux valeurs obtenus expérimentalement.