Quelques notions de base

Un graphe G = (V, E) est une paire formée d'un ensemble de sommet et d'un ensemble d'arêtes; ordre de G= |V|= n, dimension de G= |E| = m.

Pour un sommet v on note d(v) son degré, nombre d'arêtes liées à v. sont respectivement le minimum et les maximum des degrés des sommets du graphe.

On défini respectivement le voisinage d'un sommet v et la frontière d'une partie U par :

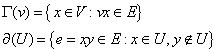
On note A la matrice d'adjacence de G et L = D-A est le laplacien combinatoire avec D matrice diagonale formée des degrés des sommets.

On note B la matrice d'incidence: B = (b_ij) où le coefficient b_ij vaut 1 si le sommet i est le sommet initial de l'arête j. Il vaut -1 si c'est le sommet final et 0 dans les autres cas. Si le graphe initial est non-orienté, une orientation arbitraire est définie afin de déterminer B.

On a L = BB' .

Si le graphe est non-orienté, A et L sont des matrices hermitiennes et L est définie semi-positive.

Si T est hermitienne, elle est diagonalisable, elle a une forme quadratique associée r(x) = <Tx,x> et ses valeurs propres sont données par :

Où x1 est un vecteur propre de la première valeur propre. Cette construction se poursuit jusqu'à la dernière valeur propre que l'on peut également obtenir par une opération de maximum.

Donc on a pour V(T), image de la sphère unité:

De plus ces valeurs propres sont positives si T est positive.

Cycles et co-cycles

On considère:

C₀(G) fonctions sur V à valeur dans un corps K

C₁(G) fonctions sur E à valeur dans K.

Les arêtes sont orientées (arbitrairement au cas où une orientation naturelle ne serait pas définie).

Pour tout cycle (chemin fermé ne passant pas deux fois par le même sommet) C on définit une fonction z_C de C₁(G) par:

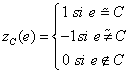
où signifie e et C ont la même orientation.

Cet ensemble de fonctions est désigné par : Z(G) .

Pour toute partition P de V = V1 U V2 on définit une fonction u_P(e) de C₁(G) par:

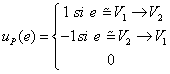
Cet ensemble est désigné par : U(G).

On a les résultats :

où k est le nombre de composantes connexes de G.

dim(Z(G)) s'appelle aussi la nullité de G .

dim(U(G)) est le rang de G

B, la matrice d'incidence, fournit une application de C1(G) dans C₀(G) et B' une application de C₀(G) dans C₁(G). On a:

ker B = Z(G) donc rang(B) = n-k

Im B' = U(G)

Connectivité

Les valeurs propres de L = D-A, le laplacien combinatoire, donnent des informations sur la structure du graphe.

1) La multiplicité de la valeur propre ₁ = 0 donne le nombre de composantes connexes du graphe.

2) Si W est un ensemble de sommets, W sépare G si G-W n'est pas connexe.

G est dit k-connecté si G est le graphe K_n+1 (graphe complet à n+1 sommets) ou si G a au moins k+2 sommets et il n'y a pas d'ensemble de k-1 éléments qui sépare G.

La connectivité de G est le maximum des k tels que G est k-connecté (il existe donc un ensemble de k sommets qui le sépare).

Notation : connectivité de G = max {k : G est k-connecté } =

Résultat 1:

Résultat 2:

3) En supposant le graphe connexe, la deuxième valeur propre est donnée par:

où x₁ est le vecteur dont toutes les composantes valent 1 (vecteur propre associé à la première valeur propre 0).

En séparant le graphe en deux selon que x_i est positif ou négatif, la formule avec les conditions donne une valeur minimum du "cut" entre les deux parties ainsi définies.

Référence : Bollodás, B. (1998). Modern graph theory. Berlin: Springer Verlag, GTM 184.