Quelques manipulations pour déterminer la structure d'un hypertexte
Introduction
Ce document montre quelques manipulations permettant de déterminer la "topologie" d'un hypertexte.
Ces manipulations sont réalisées à partir d'un hypertexte généré par le processus par degré d'attirance décrit dans le document "Un simulateur pour la création d'hypertextes" .
Topologie d'un hypertexte
Cette topologie est celle des graphes orientés dont on rappelle ici deux éléments: la structure papillon et les notions, héritées des travaux concernant le "web", d'autorité et de hub.
La structure papillon
L'ensemble des sommets (unités d'informations) d'une composante connexe peut se décomposer en 7 classes (Barabasi, 2002):
.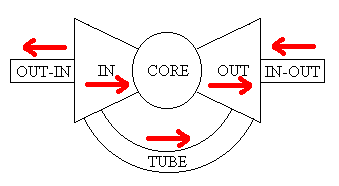
- CORE
- Pour tout couple de sommets x, y de cet ensemble, il existe un chemin de x à y et un chemin de y à x. Cet ensemble CORE n'est pas déterminé de façon unique. Un CORE peut être construit à partir de chaque sommet. Appartenir à un même CORE constitue une relation d'équivalence. La décomposition d'un hypertexte en CORE peut dans certains cas constituer une analyse de structure intéressante.
- IN
- Tous les sommets x tels qu'il existe un élément y de CORE avec un chemin de x à y.
- OUT
- Tous les sommets x tels qu'il existe un élément y de CORE avec un chemin de y à x.
- TUBE
- Les sommets atteignables depuis IN qui rejoignent OUT
- OUT-IN
- Les sommets atteignables depuis IN qui ne rejoignent pas OUT
- IN-OUT
- Les sommets non atteignables depuis IN qui rejoignent OUT
Stratification du CORE
Il est possible de définir: K+n(u), ensemble des unités d'information que l'on peut atteindre depuis u en parcourant au plus n arêtes.
De même: K-n(u), ensemble des unités d'information à partir desquelles il est possible d'atteindre u en parcourant n arêtes au plus.
Kn(u) = K+n(u) ![]() K-n(u)
K-n(u)
Les ensembles sont imbriqués: Kn(u) ![]() Kn+1(u) . A cette suite croissante correspond une suite de
graphiques tels que définis dans le document "structure
d'un hypertexte sous forme matricielle".
Kn+1(u) . A cette suite croissante correspond une suite de
graphiques tels que définis dans le document "structure
d'un hypertexte sous forme matricielle".
De plus K![]() (u)
est le CORE généré par u.
(u)
est le CORE généré par u.
Autorités et hubs
Une "autorité" est une page (ou un site) référencée par de nombreuses autres pages. Un "hub" est une page (ou un site) référençant de nombreuses "autorités". Les tandems "autorité-hub" constituent l'ossature du "web".
Dans cette définition, la notion de "hub" est subordonnée à la notion d' "autorité". Une autre acception serait de prendre "autorités" et "hubs" comme des notions duales. Cette distinction serait à préciser dans des cas pratiques pour juger de son utilité.
On pourrait aussi distinguer les "autorités", "les portails" (appelés hub précédemment) et les "hubs" qui sont à la fois portails et autorités. Pour les "hubs et les "portails", il conviendrait alors de distinguer ceux qui se réfèrent plus spécifiquement à des "autorités".
Le simulateur
Il permet de céer des unités d'information, chacune caractérisée par:
-
un numéro d'ordre;
-
son degré de 'fitness' qui représente une certaine qualité intrinsèque de l'unité. Le degré de fitness est un nombre aléatoire compris entre 0 et 1;
-
le nombre de liens émis depuis cette unité d'information;
-
son type qui donne la nature de l'unité d'information (domaine traité).
-
dis_lnk: donne la distribution du nombre de links émis par une nouvelle unité d'information (distribution normale dans l'exemple)
-
dis_typ: donne la distribution des types (distribution croissante dans l'exemple)
La matrice uis contient l'ensemble des unités d'information (une par ligne), les colonnes donnant le numéro, le degré de fitness, le nombre de liens et le type.
Les liens sont fabriqués selon un coefficient d'attirance qui dépend des types respectifs de la source et de la cible, du degré de fitness de la cible et du nombre de liens de la cible.
r est la matrice d'adjacence. rij = 1 signifie qu'il y a un lien de l'unité d'information i vers l'unité d'information j.
Exemple technique
La commande load simul initialise les variables (y compris 2 unités d'information).
Le commande agreg(13,5) ajoute 13 unités d'information, puis elle choisit 5 unités d'information à partir desquelles des liens sont établis selon le même algorithme que précédemment,
La matrice obtenue est:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
r =
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
4 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
5 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1
6 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0
7 0 1 0 1 1 1 0 0 0 0 0 0 1 0 1
8 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0
9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
10 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0
11 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
12 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0
13 0 0 0 0 1 1 0 0 0 1 1 0 0 0 1
14 0 0 0 0 0 0 1 0 0 1 0 1 1 0 1
15 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0
La commande tri_r permet d'obtenir une statistique. Pour chaque unité d'information on calcule l'ordre du sommet, le nombre de liens entrants (descripteurs) et le nombre de liens sortants (référents).
UI ordre nb de nb de
descr. réf.
7 10 4 6
5 8 6 2
15 8 5 3
13 8 3 5
6 6 4 2
12 5 2 3
10 5 2 3
14 5 0 5
4 4 3 1
2 3 2 1
11 1 1 0
1 1 1 0
8 1 0 1
3 1 0 1
9 0 0 0
66 33 33
On voit que les unités 7, 5, 15 et 13 constituent des unités centrales.
Les unités 14, 8, 3 n'ont pas de liens entrants (ce sont des sources), les unité 1 et 11 sont au contraire des puits (pas de liens sortants). L'unité 9 est isolée.
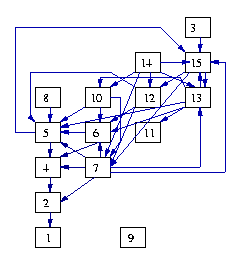
Analyse
Le but est de trouver la structure "papillon" de l'hypertexte. L'unité d'information 7 est un candidat pour la création du "CORE". En calculant la clôture transitive r + ... + r^15 (mod 2) on trouve toutes les unités d'informations qui lui sont liées.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
3 1 1 0 1 1 1 1 0 0 1 1 1 1 0 1
4 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0
5 1 1 0 1 1 1 1 0 0 1 1 1 1 0 1
6 1 1 0 1 1 1 1 0 0 1 1 1 1 0 1
7 1 1 0 1 1 1 1 0 0 1 1 1 1 0 1
8 1 1 0 1 1 1 1 0 0 1 1 1 1 0 1
9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
10 1 1 0 1 1 1 1 0 0 1 1 1 1 0 1
11 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
12 1 1 0 1 1 1 1 0 0 1 1 1 1 0 1
13 1 1 0 1 1 1 1 0 0 1 1 1 1 0 1
14 1 1 0 1 1 1 1 0 0 1 1 1 1 0 1
15 1 1 0 1 1 1 1 0 0 1 1 1 1 0 1
On observe qu'il n'est pas possible de revenir sur 7 à partir des unités d'information (1 2 4) qui sont à exclure du CORE. Finalement celui-ci se compose des unités (5 6 7 10 12 13 15).
Finalement:
-
IN = (3 8 14)
-
CORE = (5 6 7 10 12 13 15)
-
OUT = (1 2 4 11)
Automatisation du calcul
Pour rechercher le CORE d'un graphe orienté (de l'hypertexte) lorsque le nombre d'unités est important, la procédure suivante peut être proposée:
-
recherche de la fermeture transitive GB = G * (I-G/n)^(-1); [1]
-
univaluation: GB = GB & GB;
- GB(i,:)&GB(:,i) = v(j) représente le vecteur "caractéristique" du CORE engendré par l'unité d'information i (v(j) == 1 signifie l'unité j est dans CORE)
-
recherche pour chaque Ui du nombre d'unités (t(i)) qui peuvent être atteintes et qui peuvent l'atteindre. t(i) = sum(GB(i,:)&GB(:,i))
Ce processus donne donc la taille du CORE généré
par chacun des sommets du graphe (rappel si Cx et le CORE
généré par x et si y ![]() Cx alors Cx = Cy).
Cx alors Cx = Cy).
Un même processus peut être utilisé pour déterminer Kn(u) à partir de l'uniévaluation de GB + GB^2 + ... + GB^n .
Autre approche
Il est également possible d'utiliser la normalisation introduite dans le document Structure d'un hypertexte sous forme matricielle après avoir reconstruit les matrices D et R.
L'introduction d'une coupure à 0.1, montre la structure suivante:
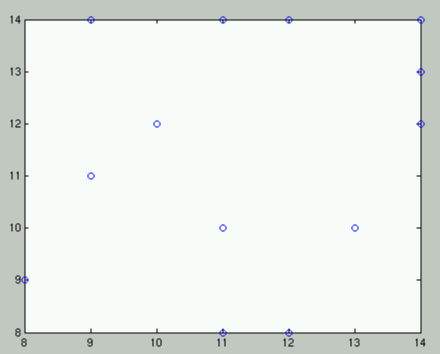
Les valeurs numériques sont les suivantes:
| UI | 7 | 15 | 5 | 13 | 4 | 6 | 10 | 12 | 14 | 2 | 8 | 3 | 1 | 11 | 9 |
| DX | 8 | 11 | 11 | 9 | 12 | 11 | 10 | 10 | 9 | 13 | 11 | 12 | 14 | 14 | 14 |
| DY | 9 | 8 | 8 | 11 | 8 | 10 | 12 | 12 | 14 | 10 | 14 | 14 | 12 | 13 | 14 |
| 17 | 19 | 19 | 20 | 20 | 21 | 22 | 22 | 23 | 23 | 25 | 26 | 26 | 27 | 28 |
où DX représente un manque en référents (la valeur 14 indique un puit) et DY un manque en descripteur (la valeur 14 indique une source).
Utilisation du laplacien combinatoire
La commande l=lap(r)calcule le laplacien combinatoire de r dont la version pleine (l1=full(l)) est:
1,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 -1, 3, 0,-1, 0, 0,-1, 0, 0, 0, 0, 0, 0, 0, 0 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,-1 0,-1, 0, 4,-1,-1,-1, 0, 0, 0, 0, 0, 0, 0, 0 0, 0, 0,-1, 8,-1,-1,-1, 0,-1, 0,-1,-1, 0,-1 0, 0, 0,-1,-1, 6,-1, 0, 0,-1, 0,-1,-1, 0, 0 0,-1, 0,-1,-1,-1, 9, 0, 0,-1, 0,-1,-1,-1,-1 0, 0, 0, 0,-1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 0, 0, 0, 0,-1,-1,-1, 0, 0, 5, 0, 0,-1,-1, 0 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0,-1, 0, 0 0, 0, 0, 0,-1,-1,-1, 0, 0, 0, 0, 5, 0,-1,-1 0, 0, 0, 0,-1,-1,-1, 0, 0,-1,-1, 0, 7,-1,-1 0, 0, 0, 0, 0, 0,-1, 0, 0,-1, 0,-1,-1, 5,-1 0, 0,-1, 0,-1, 0,-1, 0, 0, 0, 0,-1,-1,-1, 6
Les valeurs propres de l1 sont: 0 ; 0 ; 0.57 ; 0.83 etc. Il y a donc deux composantes connexes comme déjà observé (l'unité isolée 9 et le reste).
Le vecteur propre correspondant à la valeur propre 0.57 est:
1 0.82082 2 0.35583 3 -0.25851 4 0.062867 5 -0.07151 6 -0.050681 7 -0.017781 8 -0.16496 9 0 10 -0.073295 11 -0.22962 12 -0.076119 13 -0.099539 14 -0.08544 15 -0.11206
Il nous indique que outre 9 isolé, les unitiés C1 = {1, 2, 4} (coefficients positifs) forment un paquet relativement peu connecté au reste C2 = {3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15}. C'est une approximation qui minimise:
cut(C1,C2) * (1/#C1 + 1/#C2)
Approche alternative
La théorie (Kleinberg, 1997) indique que les "hubs" correspondent aux unités d'information liées aux composantes maximales du vecteur propre associé à la valeur propre maximum de la matrice d'adjacence multipliée par sa transposée. Pour les "autorités", il faut prendre le produit de la transposée par la matrice d'adjacence.
Dans notre cas r'* r et r * r' ont pour valeur propre maximum 14.6. Les vecteurs propres correspondants sont v1 et v2:
n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 v1 0 .15 0 .24 .52 .43 .32 0 0 .21 .12 .15 .29 0 .43
v2 0 0 .11 .04 .18 .20 .54 .13 0 .34 0 .34 .45 .37 .20
Les unités 5, 6, 15, 7 et 13 sont des "autorités". Les unités 7, 13, 12, 10 et 14 sont plutôt des "portails". Les unités 7 et 13 sont des "hubs". A noter que les composantes d'un des vecteurs pour les "puits", les "sources" et les unités isolées (unités 1, 2, 3, 8, 9, 11 et 14) sont nulles.
Bibliographie et notes
Barabasi, A.-L. (2002). Linked, The New Science of Networks. Cambridge, MA : Perseus Publishing.
Kleinberg, J.M. (1997). Authoritative sources in a Hyperlinked Environment. IBM Research Report RJ 10076, May 1997.
[1] En prenant n > || G ||, cela permet d'avoir
une série ![]() (G/n)i
convergente qui représente la matrice de la fermeture transitive
pondérée d'une façon ad hoc (sans importance vu
l'étape ultérieure). Sans pondération, est-il possible
de travailler avec des séries formelles (les composantes négatives
de 1/(I - G) correspondants aux séries non convergentes) ?
(G/n)i
convergente qui représente la matrice de la fermeture transitive
pondérée d'une façon ad hoc (sans importance vu
l'étape ultérieure). Sans pondération, est-il possible
de travailler avec des séries formelles (les composantes négatives
de 1/(I - G) correspondants aux séries non convergentes) ?
