Position du problème

La théorie des graphes fournit un certain nombre d'outils d'analyse qui seront appliqués aux hypertextes.

Les notations

Deux relations caractérisent un hypertexte qui donnent lieu à deux matrices D (relation document x descripteur) et R (relation document x référent).

On peut considérer le multigraphe (deux sommets peuvent être reliés par plusieurs arâtes) induit par l'hypertexte H. Il est d'ordre t, nombre d'unités d'information. Sa dimension (nombre d'arêtes) vaut:

La matrice d'adjacence du graphe est G = RD' .

Pour un sommet v on note d(v) son degré.

On note le minimum et le maximum des degrés des sommets du graphe.

Matrice d'incidence et laplacien

Classiquement pour un graphe orienté on considère B matrice d'incidence entre les sommets (donc dans ce cas, les unités d'information) et les arêtes.

B = (b_ij) où le coefficient b_ij vaut 1 si le sommet i est le sommet initial de l'arête j. Il vaut -1 si c'est le sommet final et 0 dans les autres cas.

La matrice B est de dimension t x e.

Exemple : On considère l'hypertexte déjà étudié:

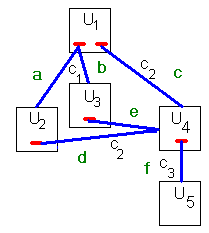
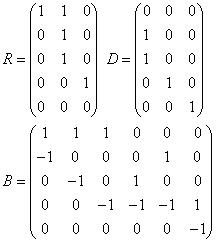
B s'obtient facilement à partir de R et D. L'algorithme est le suivant:

Construction de la matrice d'incidence B: On parcourt R ligne par ligne. Soit i la ligne courante. Si on observe un 1 en colonne j, on met sur la ligne i de B autant de 1 qu'il y en a dans la colonne j de D. Soit un de ces 1 en ligne k et colonne j de D qui a permis de placer 1 en colonne c de B. On place encore -1 dans la ligne k et colonne c.

A noter si le graphe n'est pas orienté, B est définie en ajoutant une orientation arbitraire aux arêtes. Dans notre cas on a une orientation naturelle.

On a : L = BB' = K_A-A (Laplacien combinatoire) où A = (a_ij) est la matrice d'adjacence du graphe et K_A= (k_ij) une matrice diagonale avec:

Dans le cas des graphes orientés de matrice G, on peut prendre:

A = G+G' .

Dans notre exemple, nous avons:

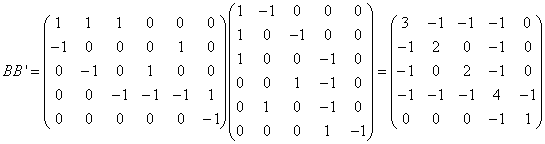
Qui vaut bien K_G+G' - (G+G') avec

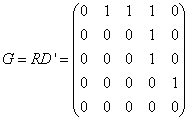
A et L sont hermitiennes, elles sont donc diagonalisables. De plus L est définie semi-positive.

Les valeurs propres de A ont les propriété suivantes :

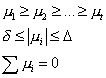
Les valeurs propres de L satisfont à:

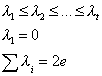
Avec e valant la dimension (nombre d'arêtes) du graphe.

Le vecteur j = (1,1,1…) correspond à la valeur propre 0 de L.

La multiplicité de la valeur propre 0 vaut le nombre de composantes connexes du graphe. En effet, dans le cas d'un graphe non connexe, L peut se décomposer sous forme de blocs, chacun représentant un graphe.

On a de plus: rang B = rang BB', donc le rang de B vaut t - k où k est le nombre de composantes connexes de G.

On a une relation entre les valeurs propres de A et celles de L lorsque le graphe est r-régulier : celles de L s'obtiennent en opposant celles de A et en ajoutant r. En effet, on a:

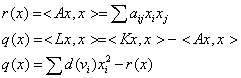
Par ailleurs, les valeurs propres de A s'obtiennent en prenant les valeurs maximum ou minimum de r(x) (avec x de module 1). Pour L, on procède de même avec q(x). Donc si le graphe est r-régulier, tous les d(v) sont égaux à r et à un maximum de q(x) correspond un minimum de r(x). Ce qui démontre la relation.

Dans le cas général, l'égalité permet de donner quelques estimations, en particulier :

Dans le cas de l'exemple ci-dessus, les valeurs numériques sont :

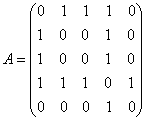
Valeurs propres de A: 2.6855 ; 0.3349 ; 0 ; -1.2713 ; -1.7491

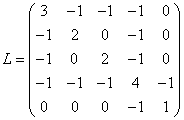
Valeurs propres de L: 0 ; 1 ; 2 ; 4 ; 5

On vérifie que la somme des valeurs propres de A est nulle et que la somme de celles de L vaut 12, le double du nombre d'arêtes du graphe.

On en déduit encore que le graphe est connexe et que sa connectivité est supérieure ou égale à 1 et que :

Conclusion

Quelques démarches proposées pour déterminer la structure d'un hypertexte dont on possède D et R :

Démarche 1) On cherche B (matrice d'incidence). La multiplicité de la valeur propre 0 de BB' donne le nombre de composantes connexes de l'hypertexte. Cette proposion ne tient pas compte de l'aspect pondération. On peut faire de même à partir de la matrice pondérée rendue symétrique

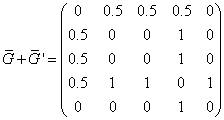
Les valeurs propres sont 2.0301 ; 0.2569 ; 0 ; -0.5529 ;-1.734. Leur somme est nulle. Ces valeurs se rapprochent de celles de A.

On peut également construire le laplacien de la matrice précédente:

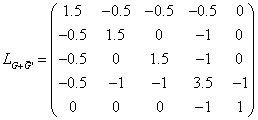
Les valeurs propres sont 0 ; 0.0511 ; 0.3962 ; 0.4472 ; 0.8003

Démarche 2) On calcule les matrices suivantes :

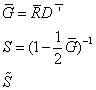
Cette dernière matrice est dichotomisée et symétrisée par addition de sa transposée. On obtient A dont on met la diagonale à 0. Puis on fabrique L. Le graphe dichotomisé a plusieurs composantes connexes que l'on peut étudier du point de vue orienté.

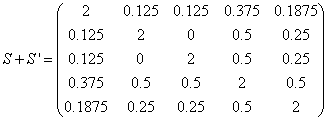
Les valeurs propres sont 3.2122 ; 2 ; 1.8689 ; 1.6751 ; 1.2439

Les valeurs propres de avec les valeurs de la diagonale mises de telle manière que la somme des lignes soit nulle valent : 0 ; 0.875 ; 0.9711 ; 1.4244 ; 2.3545 . En soit ce résultat n'est vraisemblablement pas intéressant.

C'est plus intéressant lorsque S est tronqué à 0.2 puis dichotomisé:

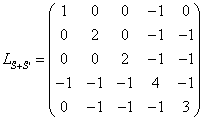
Les valeurs propres sont: 0 ; 1 ; 2 ; 4 ; 5 comme celles de L, bien que la structure soit différente !

Dans le cas de l'hypertexte des "utopies à construire" on trouve 213 valeurs propres de L "tronqué" à 0.1 et dichotomisé.

Ces valeurs propres (entre parenthèse leur multiplicité) sont tout d'abord:

0 (127) , 1 (3), 3 (3), 5 (2), 6, 7 (2), 8 (2) ;

puis 73 valeurs sont non entières variant de 1.155 à 20.217

Cet hypertexte contient donc beaucoup d'unités d'information assez isolées (les notes et références).

Démarche 3) Etude de la connectivité à l'aide de la deuxième valeur propre.

Reste encore à trouver une manière de repérer les unités isolées ou centrales, les "ponts" et les unités "séparatrices".