Introduction aux systèmes à base de connaissances
CHAPITRE II : Applications et méthodes
Quelques domaines d'application des systèmes à base
de connaissances
Les thèmes abordés par l'IA sont multiples. Ils
concernent aussi bien le logiciel que le matériel. Un projet
complet (par exemple le projet japonais dit de 5e
génération) mêle souvent plusieurs types de
préoccupations (programmation, interfaçage, architecture
des ordinateurs, conception des circuits, etc.). Voici les
catégories principales:
Traitement du langage naturel: contrairement à ce
que l'on croyait initialement (et naïvement), la traduction
automatique demande plus que la fabrication de dictionnaires et
l'utilisation de règles de syntaxe. Traduire un texte
nécessite une compréhension du texte ou, pour le moins,
une certaine représentation qui fait intervenir le contexte, une
connaissance experte de la matière et un certain sens commun.
Une anecdote souvent citée par les chercheurs dans le domaine
est la double traduction de l'anglais en russe puis de russe en anglais
de: "The spirit is willing, but the flesh is week" qui devenait: "The
vodka is good, but the meet is rotten"
Actuellement le traitement du langage (traduction automatique,
génération automatique de textes, analyse du langage
naturel, ...) introduit de multiples outils:
- Utilisation de SCRIPTS qui sont des séquences standard de déroulement d'un dialogue;
- Représentation par dépendance conceptuelle (voir plus loin);
- Réseaux neuronaux
Plus que de traduction automatique on parle maintenant de traduction
assistée !
Recherche dans des bases de données: il s'agit de
dépasser la recherche par motsclés pour effectuer
des recherches à partir de demandes effectuées en langage
naturel. L'ordinateur assiste l'utilisateur dans sa démarche.
Assistance: c'est l'application commerciale principale
des systèmes à base de connaissances. Il s'agit du
domaine des systèmes experts qui sont caractérisés
à la fois par une fonction (assistance qui peut remplacer celle
d'un expert) et par un certain type de systèmes informatiques.
Le fonctionnement d'un système expert est prototypique des
systèmes à base de connaissances.
Démonstration de théorèmes
mathématiques: c'est un sujet classique qui a permis de
développer les principales méthodes d'IA. Plusieurs
langages de programmation utilisés en IA sont basés sur
les techniques utilisées dans ce domaine (PROLOG, PLANNER).
Planning: ce sujet est également important dans le
développement de l'IA. Un but est proposé, et
l'ordinateur doit trouver l'ensemble des étapes qui permettent
de l'atteindre. La robotique de même que la gestion de production
est largement tributaire des recherches menées dans ce domaine.
Programmation automatique: il s'agit de la
réalisation de programmes à partir de la description des
fonctions à remplir. Sorte de "supercompilateurs", ces
systèmes s'achoppent à des problèmes ardus
d'optimisation (reconnaître que plusieurs procédures sont
équivalentes). Actuellement plusieurs systèmes
d'assistance à la programmation existent (environnements de
génie logiciel). Ils sont liés souvent à une
méthodologie générale de résolution de
problème (SMXCogitor).
Résolution de problèmes: il s'agit
principalement de problèmes à base de combinatoire
(parcours, jeux ,...). Le travail consiste à modérer au
maximum l'"explosion combinatoire". C'est dans ce domaine que l'on
trouve un des premiers programme, le plus "fameux" de l'IA, le General
Problem Solver (GPS) de Newell, Simon et Shaw (1957). Le GPS
résout onze types de problèmes: problèmes
d'échec, intégration symbolique, puzzle,... Il n'est pas
aussi efficace que les programmes spécialisés mais avait
été conçu pour être "une série de
leçons donnant une meilleure vue de la nature de
l'activité de résolution de problèmes ainsi que
des mécanismes à mettre en jeu en vue de leur
accomplissement".
La structure du GPS est prototypique des systèmes basés
sur des recherches combinatoires. On donne des DONNEES, un BUT et des
opérateurs. Le système applique les opérateurs aux
données afin de réduire la différence entre
données et but. ALICE (Laurière, 1978) est un
système essentiel de résolution de problèmes. Une
certaine heuristique est introduite pour tenter de réduire la
combinatoire. Actuellement une perspective des plus prometteuses est la
résolution de problèmes assistée par ordinateur.
Perception: ici, il s'agit d'identifier des objets
complexes. Ce qui ne peut se faire que par un jeu d'hypothèses
et de tests. Regarder n'est pas voir, écouter n'est pas
entendre. Les systèmes qui regardent et écoutent doivent
faire des hypothèses sur ce qui est vu ou entendu et
procéder à des vérifications. Cela suppose
également un grand nombre de connaissances à disposition
du système. La technique des réseaux neuronaux s'impose
de plus en plus dans ce domaine.
- Enseignement assisté par ordinateur: des techniques
d'intelligence artificielle peuvent être introduites dans des
tutoriels. Les tutoriels intelligents sont constitués de
plusieurs systèmes experts travaillant en collaboration. En
particulier:
- système expert du domaine: il est capable de résoudre les problèmes qui sont soumis aux élèves. Ce système est capable de calculer les réponses et de trouver des erreurs caractéristiques.
- système expert de didactique: il choisit les questions à soumettre aux élèves et analyse les démarches et erreurs éventuelles.
- système expert psychologue: il est chargé de réaliser un profil de l'élève.
Représentation des connaissances
Les connaissances sont des données qui contrairement au
données classiques ne sont pas seulement des informations
statiques, mais indiquent des traitements à faire effectuer
à d'autres données plus élémentaires. Les
procédures de la programmation classique constituent un type de
connaissance (connaissance procédurale). Voici d'autres modes de
représenter et de stocker des connaissances:
Calcul des propositions et prédicats
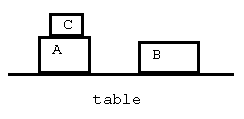
On peut représenter la situation de la figure de la
manière suivante en utilisant les prédicats 'sur',
'surtable', 'libre':
| sur(C,A) surtable(A) surtable(B) libre(C) libre(B) |
 |
Par ailleurs, à l'aide d'opérateurs de la logique du
premier ordre, il est possible de définir de nouveaux
prédicats: 'oter', 'empiler' et de donner des
équivalences:
1) libre(x) <==> ¬ ( y sur(y,x)) (il n'existe pas
de y sur x)
2) sur(y,x) ^ oter(y,x) ==> libre(x) ^ ¬ sur(y,x)
3) libre(x) ^ libre(y) ^ empiler(x,y) ==> sur(x,y)
Il est possible de donner un but à atteindre (par un robot) de
la même façon, par exemple: sur(A,B). A partir de cette
information et de la règle 3 le système déduit
libre(A), libre(B) et empiler(C,A). La règle 2 conduit à
l'action oter(C,A).
Réseaux sémantiques
Il s'agit de réseaux dont les noeuds représentent les
concepts et les arcs représentent les relations. Le but des
réseaux sémantiques est de fournir une
représentation souple des connaissances. Un exemple d'un tel
langage de description est par exemple FRL qui exploite la notion de
"frame" élaborée par Marvin Minski (Roberts, R.B,
Goldstein, I.P. (1977) The FRL Primer. MIT: Memo 408).
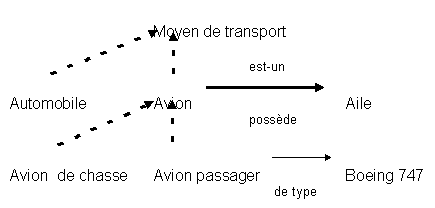
On utilise de façon fondamentale les propriétés
des relations: par exemple:
la transitivité (est-un est une relation transitive),
héritage via d'autres relations (le Boeing 747 a des ailes),
relations réciproques (le Boeing 747 est un avion passager).
Dépendance conceptuelle
La dépendance conceptuelle est une technique qui permet
d'analyser le sens d'une phrase en recherchant tous les
éléments qu'elle est sensée représenter.
Plus spécialement, elle essaie de concrétiser tout ce qui
est sousentendu. Cette technique a été introduite
par R. Schank et son équipe [SCHANK].
Leur démarche est celleci: au lieu de s'attacher sur le
sens précis de chacun des mots de la langue, ils
considèrent le sens d'une phrase dans sa globalité et,
c'est ce sens qu'ils essaient de représenter. Leur
théorie vient de la constatation que dans une phrase anglaise,
beaucoup d'éléments étant sousentendus,
ceuxci doivent être connus et devinés par celui qui
veut interpréter le sens de la phrase. Dans leur
représentation du sens, ils cherchent à combler les
lacunes laissées par ces éléments
sousentendus. Ils considèrent une phrase comme un
événement ayant un acteur, un objet, une action
réalisée par l'acteur sur l'objet et une direction vers
laquelle cette action est orientée. La représentation de
la structure d'un événement est invariable.
Chaque événement a:
un ACTEUR
une ACTION réalisée par cet acteur
un OBJET sur lequel est réalisée l'action
une DIRECTION vers laquelle cette action est orientée
Un acteur est un objet concret qui peut "décider" d'agir sur un
autre objet concret.
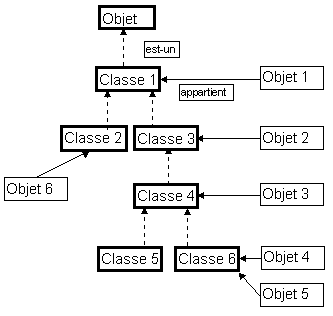
Langage à objets
L'origine de langage objet peut être trouvée dans les
réseaux sémantiques. En fixant une relation
hiérarchique de base (est-un) et une relation d'appartenance
(appartient-à), on a la structure d'un langage objet. Les autres
relations se cachent dans les attributs des entités. Les
entités hiérarchisées sont les classes (avec au
sommet une classe racine souvent appelée OBJET). Les autres
entités, les objets proprement dits, appartiennent aux
différentes classes.
L'idée de langage à objets connaît différents types d'implémentations ayant chacune ses caractéristiques avec quelques dénominateurs communs. Les premiers objets ont été définis comme une structure de données en LISP (les flavors). SMALLTALK est un des premiers langages qui a mis systématiquement en oeuvre cette méthode et constitue le modèle prototypique et le plus complet des langages à objets. Des langages classiques ont ajouté cette possibilité à leur noyau habituel (Turbo PASCAL dès la version 5, c++). Une version objet de COBOL est même annoncée (Grehan, R. (1994) Object-Oriented COBOL. BYTE, vol 19 no 9, septembre 1994). Cette notion permet aussi d'organiser des systèmes de présentation multimédia (HYPERCARD, TOOLBOOK). MODULA, OBERON et surtout ADA, par leur modularité, possèdent également de nombreuses caractéristiques des langages à objets.
L'exemple suivant, permettra de définir quelques concepts:
classe rectangle:
Variables:
- (longueur (valeur: un nombre))
- (largeur (valeur: un nombre))
- (coin (valeur: un point))
Méthodes:
- (aire (* longueur largeur))
- (display (draw-rect (centre longueur largeur)))
- (init (a b)(setq longueur a)(setq largeur b))
La classe des rectangles, sous-classe de la classe racine, est
définie par 3 variables d'instance (champs) et trois
méthodes. Les méthodes sont des procédures
liées à la classe, identifiée par un
sélecteur (ici aire, display, init). Pour utiliser ces
procédures, il s'agira d'envoyer des messages aux objets de la
classe. En principe, aucun accès direct aux données d'un
objet n'est possible (encapsulation). La classe des points est
donnée par:
classe point:
Variables:
- (cx (valeur: un nombre))
- (cy (valeur: un nombre))
Méthode:
- (display (plot (cx cy))
- (init (a b)(setq cx a)(setq cy b))
(rectangle new rec-1) ; définit l'objet rec-1, instance de la
classe des rectangles
(rec-1 init 25 10 pointA) ; initialise les valeurs de rec-1 (coin
pointA supposé défini,
; dimension 25x10)
(rec-1 aire) -> 250 ; ce message permet d'obtenir la valeur de
l'aire de rec-1
On notera que la méthode init est différente selon
l'objet auquel elle s'applique (polymorphisme).
On peut considérer une sous-classe de la classe des rectangles:
classe rectangle-remplis: (un rectangle)
Variable:
(couleur (possibilités: jaune bleu rouge))
Méthode:
(display (super display)(fill couleur))
(init (a b c)(super init a b)(setq couleur c))
Cette nouvelle classe possède les propriétés et
les méthodes de la classe des rectangles. Par ailleurs, les
méthodes display et init sont redéfinies en utilisant la
partie existante dans la classe au-dessus (réutilisation du
code). super est l'objet lui-même considéré comme
membre de la classe mère. Il se référence par self
comme élément de sa propre classe.
En résumé, un objet est déterminé par
différent attributs déterminés dans sa classe.
Chaque attribut peutêtre typé (ici) ou non.
Par la possibilité de définir des classes d'objets
emboîtées, on utilise de façon fondamentale les
mécanismes d'héritage. Dans les exemples ci-dessus
l'emboîtement est défini à l'aide de "un/une".
Dans les langages "objet", les procédures qui spécifient
le comportement des classes reçoivent le nom de
"méthodes". Les objets communiquent par l'envoi de messages qui
invoquent les méthodes à mettre en oeuvre. Avec
différentes nuances, la syntaxe de cet envoi de message est: objet
message paramètres.
Les langages de l'intelligence artificielle
Les langages utilisés en Intelligence artificielle
présentent diverses caractéristiques communes:
ils constituent un environnement interactif,
ils privilégient le sens à la structure,
ils sont extensibles,
ils possèdent une structure de données très
dynamique: les listes.
Les principaux langages généraux sont Lisp (avec ses
divers dérivés: Logo, muSIMP), Prolog et Smalltalk
(langage objet). Le premier est applicatif, Prolog est un langage
déclaratif. Quant à Smalltalk c'est un langage par
objets. Il existe de nombreux langages dédiés à
des applications particulières.
Le langage LISP
Le langage LISP a été conçu par John McCarthy
entre les années 1956 et 1958. Une première implantation
du langage (version 1.5) a été réalisée au
MIT sur un ordinateur IBM 704 entre 1958 et 1962. Il existe plusieurs
versions de LISP. Une référence est Common Lisp [STEELE]
qui est compatible avec de nombreuses implantations et dont d'autres
tentent de s'approcher: Le_Lisp [CHAILLOUX]. Une version
intéressante, du domaine public, XLISP. Une version
orientée pour l'enseignement est SCHEME.
Les objets du langage sont principalement les atomes: qwerty, a2; les
nombres: 123.8; les listes: (3 et 4 donnent 7). Toutes les
manipulations de données s'effectuent à l'aide de
fonctions. Quelques exemples:
(plus 3 4) > 7
(car '(3 et 4 donnent 7)) > 3
(cdr '(3 et 4 donnent 7)) > (et 4 donnent 7)
Les opérateurs peuvent s'enchaîner: (car (cdr '(3 et 4
donnent 7))) > et
Le Lisp est caractérisé par l'équation
Données = Programmes. En effet les programmes sont des listes.
Il existe une fonction (eval) qui permet d'évaluer une liste en
tant que programme. En Lisp, programmer consiste à
définir de nouveaux opérateurs.
Exemple, la fonction fibo
La suite de fibonacci 1, 1, 2, 3, 5, 8, 13, 21, ... est
donnée par: fibo(0) = 1, fibo(1)=1 et la relation: fibo(n)=
fibo(n-1) + fibo(n-2). Sa définition en Lisp est:
(defun fibo (n)
(cond ((< n 2) 1)
(t (+ (fibo (- n 1))
(fibo (- n 2))))
)
)
Les systèmes Lisp comptent de quelques dizaines
d'opérateurs primitifs à plus de mille.
Le langage Prolog
Les objets primitifs sont du même type qu'en Lisp, les
atomes, les nombres et les listes ([3,et,4,donnent,7]).
Programmer c'est "déclarer" des assertions ou des faits,
définir des règles et poser des questions.
précieux(or).
précieux(diamant).
substance(or,métal).
substance(diamant,minéral).
sont des faits bâtis sur les prédicats: précieux,
substance, etc. Ils se lisent: l'or est précieux, l'or est un
métal, etc. Ces prédicats correspondent aux tables des
systèmes relationnels.
Il est possible d'effectuer des requêtes, par exemple:
? précieux(or) > yes (la requête pour
savoir si l'or est précieux a abouti)
?- précieux(argent) --> no (elle a échoué)
?- précieux(X) --> X=or, X=diamant (la requête abouti
et lie X aux valeurs possibles)
Les requêtes peuvent s'enchaîner:
?précieux(X),substance(X,Y) (de quelle substance (Y) sont
les choses précieuses (X))
Il est possible de donner des règles, par exemple:
même_substance(X,Y) :- substance(X,Z),substance(Y,Z)
qui se lit même_substance(X,Y) si substance(X,Z) et
substance(Y,Z) et qui signifie: X et Y sont liés par
même_substance si ils ont même substance (Z).
Fibo en Prolog
fibo(N,1):,N<2,!.
fibo(N,R):
N1 is N1,N2 is N2,
fibo(N1,R1),fibo(N2,R2),
R is R1+R2.
Il met en évidence la "coupure": "!" et l'opérateur
d'évaluation: "is".
LOGO et muSIMP
Ils sont semblables à Lisp. Une liste en mu-SIMP
s'écrit: (4.(et.(3.(font.7)))) (c'est la forme archaïque
des paires de Lisp). En Logo on a: [4 et 3 font 7]
Le programme FIBO en mu-SIMP
FUNCTION FIBO(N)
WHEN N<2, 1 EXIT,
FIBO(N1)+FIBO(N2),
ENDFUN;
Le programme FIBO en LOGO
POUR FIBO :N
SI N<2 SORS 1
SORS SOMME FIBO :N1 FIBO :N2
FIN
Le langage SMALLTALK
C'est le prototype des langages à objets. SMALLTALK est un
environnement livré avec plusieurs centaines de classes
prédéfinies et des outils (browser) qui permettent de
l'enrichir, donc de développer des applications. Pour
définir la fonction de Fibonacci en SMALLTALK, il faut
sélectionner la classe Integer et ajouter une méthode du
type:
fibonacci
^self < 2
ifTrue: [1]
ifFalse: [(self-1) fibonacci (self-2) fibonacci]
Le calcul du dixième nombre de fibonacci se fera en invoquant
sur un nombre la méthode de sélecteur fibonacci: 10
fibonacci. La méthode renvoie (^) le résultat de l'envoi
du message fibonacci au nombre 10.
Acquisition de la connaissance
La réalisation d'un système à base de
connaissances ne diffère pas fondamentalement de celle d'un
système informatique classique. L'analyse fait toutefois appel
au travail d'un nouveau type de professionnel de l'informatique, le
"cogniticien" (de cognoscere, connaître). La présentation
des méthodes dépasse le cadre de cette introduction. Le
lecteur intéressé pourra se référer
à [GALLOUIN].
A partir des connaissances d'un ou de plusieurs experts, par un
processus d'élicitation, on obtient des informations encore non
formalisées. Par modélisation, on élabore une
connaissance formelle qui sera codée. On distingue
différents types de connaissances:
- Connaissance d'environnement de tâche: comment la connaissance
est liée à l'environnement (senseur, ...).
- Connaissance de compétence: c'est ce qui est connu, les
théories et les trucs pratiques concernant le domaine.
- Connaissance de performance: il s'agit de la manière dont la
connaissance est appliquée.
Méthodes d'élicitation des connaissances
Plusieurs méthodes existent pour analyser le travail de
l'expert:
- Analyse de tâches familières par observation de cas
réels. Cela permet d'avoir des informations sur l'environnement
de tâche.
- Résolution de cas hypothétiques. Cette phase apporte en
plus des informations sur la connaissance de compétence.
- Finalement, l'étude de cas difficiles complète le tout
en apportant des informations sur le troisième type de
connaissance.
Ces diverses analyses sont réalisées à partir
d'interview, de la réalisation de tâches spéciales,
d'apport d'informations diverses, de la description des processus
obligés, de brainstorming, d'analyse de prise de
décisions et du choix effectué à partir de la
comparaison de diverses méthodes.
Plus précisément l'analyse des buts permet d'avoir des
informations de contexte. La classification des problèmes
rencontrés mène à une identification de la
connaissance. Le choix des termes primitifs et des relations, la
classification d'heuristiques permet de choisir les concepts
(l'architecture) et fournit une première description informelle.
La définition de l'espace de recherche et des méthodes
fournit une formalisation qui permet l'implémentation, les tests
et la réalisation du système.
A noter encore que l'on distingue parfois
- la connaissance descriptive que constituent descriptions verbales,
des conceptions d'apprentissage, des explications d'organisation;
- la connaissance historique: rapport d'expériences
passées, diagnostic exploratoire, script, séquence;
- la connaissance métaphorique constituée des
alternatives, des images associées, des traits
caractéristiques;
- la connaissance empirique qui est constituée des "coups de
main". C'est une connaissance implicite. Elle se formalise souvent par
des règles de production "si condition alors action";
- la connaissance théorique qui est déjà
formalisée dans les manuels ou des articles scientifiques.
Principales techniques
Techniques de recherches
Pour fixer les idées nous prenons l'exemple (simple !) du
Taquin qu'il s'agit de remettre en ordre:
1 4 5
3 2 x
6 8 7
La structure de l'objet est simple, c'est un tableau à 9
éléments. L'espace de recherche est constitué de
tous les états possibles du taquin (cet espace contient 9!
éléments). Ensuite on définit le ou les
opérateurs qui permettent d'agir sur chaque état. Pour le
taquin il y a quatre opérateurs (déplacer la case vide en
haut, en bas, à gauche ou à droite). Chaque
opérateur est accompagné de ses conditions d'application
(l'opérateur "à droite" ne peut pas être
appliqué lorsque la case vide est à droite du taquin).
Ensuite, il suffit d'appliquer systématiquement les
opérateurs en chaîne pour arriver au but fixé. Le
nombre de possibilités est tellement énorme (c'est un
phénomène connu sous le nom "d'explosion combinatoire")
que de nombreuses méthodes ont été
imaginées pour réduire le nombre de cas à
envisager. Chacune de ces méthodes a des avantages en temps de
recherche et en ressource mémoire. Mais chacune a aussi ses
inconvénients. En particulier, toutes ne conduisent pas
forcément à la solution ou à la meilleure solution.
La méthode la plus simple est connue sous le nom de "hill
climbing". Elle demande d'introduire une "fonction d'évaluation"
qui donne une appréciation sur l'état obtenu. Dans le cas
du taquin on peut définir cette fonction par: nombre de
pièces bien placées. La méthode du "hill climbing"
propose de ne considérer que les opérateurs qui
améliorent la situation du point de vue de cette fonction. Vous
pouvez vous rendre compte que cette méthode ne donne pas
toujours la solution avec le taquin, puisqu'il faut parfois commencer
par bouger des chiffres bien placés avant de pouvoir les
remettre à leur place. Différentes méthodes sont
expliquées dans [WINSTON].
Technique du Backtrack
C'est une stratégie de recherche utilisée pour
générer des états possibles. Elle correspond
à une stratégie "depthfirst" (voir plus loin). C'est
une stratégie économe en temps et en mémoire dans
la mesure où les chemins explorés ne sont pas
mémorisés. Elle s'avère efficace lorsque quelques
centaines de cas sont à envisager.
Structure générale: on possède un état
(ETAT) et un ensemble d'opérateurs ou de règles de
transformations. L'algorithme qui construit une liste
d'opérateurs (CHEMIN) menant à un but (BUT) fixé
est le suivant:
Procédure BACKTRACK (ETAT)
1. Si ETAT = BUT on retourne une liste vide ()
2. Si ETAT ne peut pas mener à la solution BACKTRACK
échoue
3. On recherche les règles applicables et on en constitue une
liste: REGLES
4. Début de boucle: si REGLES est vide BACKTRACK échoue
5. R < première des REGLES; REGLES <
reste des REGLES
6. ETAT1 < R(ETAT)
7. BACKTRACK(ETAT1)
8. En cas d'échec retour à 4,
sinon on appelle CHEMIN la liste d'opérateur retournée
par BACKTRACK(ETAT1), on place R comme premier élément de
CHEMIN et on retourne cette nouvelle liste.
Exemple d'application: coloriage d'une carte avec 4 couleurs. Pour
qu'une carte soit acceptable, deux régions adjacentes ne doivent
pas avoir la même couleur. Nous allons illustrer l'algorithme en
considérant l'exemple suivant:
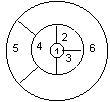
ETAT INITIAL = (1) (la première région a la couleur 1).
BUT une liste constituée de 5 valeurs (couleur des
régions 1, 2, 3, 4, 5, 6) satisfaisant la contrainte des
régions adjacentes.
Il y a 4 règles: R1 mettre la couleur 1 à la
région suivante, R2 mettre la couleur 2 à la
région suivante, R3 mettre la couleur 3 à la
région suivante et R4 mettre la couleur 4 à la
région suivante.
BACKTRACK est appliqué à l'état initial (les
numéros se réfèrent aux différentes
étapes de la procédure):
3. Les règles R2, R3, R4 sont sélectionnées
5,6. On attribue la couleur 2 à la région 2: ETAT1 = (1,2)
7. La solution est BACKTRACK de (1,2) précédé de R2
3. Les règles R3, R4 sont sélectionnées
5,6. On attribue la couleur 3 à la région 3: ETAT1 =
(1,2,3)
7. La solution est BACKTRACK de (1,2,3) précédé de
R3
3. La règle R4 est sélectionnée
5,6. On attribue la couleur 4 à la région 4: ETAT1 =
(1,2,3,4)
7. La solution est BACKTRACK de (1,2,3,4) précédé
de R4
3. Les règles R1,R2,R3 sont sélectionnées
5,6. On attribue la couleur 1 à la région 5: ETAT1 =
(1,2,3,4,1)
7. La solution est BACKTRACK de (1,2,3,4,1)
précédé de R1
3. Aucune règle n'est applicable
5,6. On attribue la couleur 2 à la région 5: ETAT1 =
(1,2,3,4,2)
7. La solution est BACKTRACK de (1,2,3,4,2)
précédé de R2
3. La règle R1 est sélectionnée
5,6. On attribue la couleur 1 à la région 6: ETAT1 =
(1,2,3,4,2,1)
7. La solution est BACKTRACK de (1,2,3,4,2,1)
précédé de R1
1. Le but est atteint.
7*. La solution est R1
7*. La solution est (R2, R1)
7*. La solution est (R4, R2, R1)
7* La solution est (R3, R4, R2, R1)
7* La solution à partir de (1) est (R2, R3, R4, R2, R1)
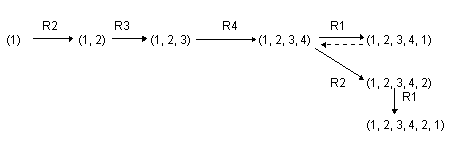
Utilisation d'arbres de recherche
Les arbres de recherche sont utilisés pour pouvoir garder en
mémoire les différentes étapes d'une recherche.
Un arbre peutêtre construit en créant des noms pour
chaque noeud (NOEUD1, NOEUD2, ...) et en mémorisant pour chacun
les informations nécessaires (état, évaluation,
nom du noeud père, ...).
On peut aussi directement utiliser la structure de liste. Ainsi l'arbre

L'arbre peut être parcouru de deux façons
différentes: en profondeur d'abord (depth first) ou en largeur
d'abord (breadth-first)
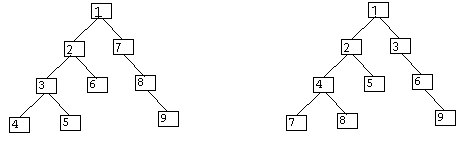
Voici l'algorithme d'une recherche en "largeur d'abord":
1) Former une liste dont le seul élément est
l'état initial
2) Faire jusqu'à ce que la liste soit vide ou que le but soit
atteint:
2a) Si le premier élément de la liste est le but ne rien
faire
2b) Sinon ôter le premier élément de la liste et
ajouter ses "descendants" à la fin de la liste.
3) Succès ou échec
Diverses variantes existent:
1) A chaque étape la liste est triée selon un
critère fournit par une fonction d'évaluation,
2) Suppression des états semblables,
D'autres fois ce sont les chemins parcourus qui sont
mémorisés.
Exercice: Dessiner l'arbre de recherche concernant le
problème du taquin. Noter pour chaque noeud la fonction
d'évaluation donnée par: E(état) = profondeur +
nombre de pièces mal placées.
Filtrage (pattern matching)
La technique de filtrage est destinée à comparer deux
objets entre eux ou un objet à un modèle. Par exemple, la
fonction donnée (filtre) regarde si un objet (son
deuxième argument) est conforme au modèle (son premier
argument). La fonction filtre est un prédicat, la valeur
rendue est VRAI ou FAUX. Par exemple, en Lisp:
(defun filtre (pattern fait)
(cond ((null pattern) (not fait) )
((equal (car pattern)(car fait))
(filtre (cdr pattern)(cdr fait)) )
((atom (car pattern)) nil)
((and (equal (caar pattern) '?)
(filtre (cdr pattern)(cdr fait)))
(set (cadar pattern)(car fait)) ) ) )
(filtre '(1 2 3)'(1 2 3)) -> t
(filtre '(1 2 3)'(3 2 1)) -> nil
Le modèle peut contenir des caractères "joker" : (filtre
'(1 2 (? X)) '(1 2 3)) -> t. Dans ce dernier cas, X sera lié
à 3. C'est un effet de bord connu sous le nom de capture.
Exercice:
1) Complétez filtre en introduisant un joker sans
capture: (filtre '(1 2 3) '(1 2 ?)) -> t
2) Complétez filtre pour qu'elle admette les
prédicats: (filtre '(numberp a 3) '(1 a 3))-> t
3) Imaginez l'utilisation de la fonction filtre pour simuler un
dialogue avec l'ordinateur. Par exemple: reconnaître un
prénom dans une phrase.
4) Esquissez un programme de la fonction inverse utilisant la fonction
filtre: (inverse '(1 2 3)) -> (3 2 1)
5) Réalisez un programme qui met des propositions courantes sous
forme canonique: tout homme est mortel --> si x homme alors x mortel
aucun animal ne sait le français --> si x animal alors x ne
sait pas le français
Jean est un garçon --> Jean garçon