Introduction aux systèmes à base de connaissances
CHAPITRE I: Introduction aux systèmes experts
Présentation
La technique des systèmes experts est de plus en plus
utilisée en informatique. Couplée souvent avec d'autres
méthodes plus classiques et éprouvées, elle permet
d'imaginer des systèmes informatiques dans des domaines
où les décisions sont soumises à des
critères complexes et évolutifs qui se laissent
difficilement aborder par des algorithmes.
Ce chapitre d'introduction devrait vous permettre de vous familiariser
avec ces instruments. Il introduit un certain langage propre au domaine
de l'intelligence artificielle.
Le dossier "pratique d'un système expert" présente un
système simple qui vous permettra de voir comment gérer
et d'utiliser les connaissances d'un expert dans des cas simples.
Généralités sur les systèmes experts
Eléments de logique des propositions
Les théories qui ont présidé à la
conception des systèmes experts sont multiples: informatique,
psychologie, logique. La logique, en particulier, fourni un langage
pratique pour présenter les systèmes experts (SE).
Quelques définitions méritent donc d'être faites,
même si, par la suite, les notions introduites ne sont pas
utilisées de façon stricte.
Voici des propositions:
P1: "les bébés pleurent quand ils ont faim"
P2: "il pleut"
P3: "je prends mon parapluie"
P4: "il neige"
P5: "les roses sont bleues"
P6: "s'il pleut, je prends mon parapluie"
Ces expressions sont considérées indépendamment du
fait de savoir si elles sont vraies ou fausses. La validité
d'une proposition P quelconque est donnée par sa "valeur de
vérité" : val(P). La valeur de vérité est
donc une fonction de l'ensemble des propositions sur l'ensemble
à deux éléments: "vrai" et "faux".
La valeur de vérité d'une proposition peut
dépendre du lieu, de l'époque, etc. Par exemple val(P5) =
faux (!). On peut aussi associer à chaque proposition une valeur
numérique représentant un degré de certitude.
A partir de propositions, il est possible de construire d'autres
propositions à l'aide de diverses opérations. En
particulier:
La conjonction (ET, ^). Exemple: P2 ^ P3 : "il pleut et je prends
mon parapluie"
La négation (NON, ¬) . Exemple: ¬P4: "il ne neige
pas"
La disjonction (OU, v ). Exemple: P2 v P4 : "il pleut ou il neige"
L'implication (SI ... ALORS, >) . Exemple: P2 >
P3(= P6)
Ainsi les propositions se combinent entre elles. C'est en ce sens que
l'on parle d'"algèbre" des propositions.
Si val(P) est connue et si val(Q) est connue également, alors il
n'est pas possible d'associer une valeur de vérité
arbitraire à l'une de leur combinaison. Ce sont des "tables de
vérité" qui indiquent, par exemple, la valeur de val(P ^
Q) connaissant val(P) et val(Q) (voir le cours de mathématique).
Une autre notion introduite par la logique, plus importante encore, est
celle de règle d'inférence (ou règle de
déduction logique). On retiendra deux règles
d'inférence:
Le Modus Ponens: Si val(P) = vrai et val(P>Q) =
vrai on en déduit: val(Q) = vrai.
C'est ce mode de raisonnement qui nous indique que si "il pleut" et que
"chaque fois qu'il pleut, Monsieur Simon prend son parapluie", alors
"Monsieur Simon doit être muni actuellement de son parapluie"
Le Modus Tollens: Si val(P>Q) = vrai et val(Q) =
faux on en déduit: val(P) = faux.
Par la suite on introduira le vocable de FAIT pour les propositions de
base et l'on dira qu'une implication P > Q est une REGLE. P est
appelée la prémisse de la règle et Q la conclusion.
Examen d'un exemple
Voici les instructions (extrait) qui permettent de
déterminer la nature d'une panne de démarreur
(tirées de Volkswagen ServiceRepair Handbook, Clymer
Publications, Los Angeles 1974).
"... Premier cas: le démarreur ne fonctionne pas ou fonctionne
au ralenti. Dans ce cas, il est proposé d'allumer les grands
phares. Si ceuxci sont faibles, c'est un problème de
batterie.
Si les phares fonctionnent normalement, on propose alors d'essayer de
faire démarrer le moteur avec les phares allumés.
Si la lumière baisse, il y a un courtcircuit dans le
démarreur. Par contre, si la lumière des phares n'est pas
modifiée, on propose de relier alors les deux grandes bobines.
Si le moteur part, il y a un problème de bobine. Sinon la panne
est autre.
Deuxième cas: le démarreur fonctionne, mais
n'entraîne pas le moteur. C'est alors un problème de
pignon..."
On trouve dans cette exemple des faits, par exemple:
F1: "le démarreur ne fonctionne pas"
F2: "les grands phares sont faibles"
F3: "problème de batterie"
Une règle relie ces trois faits:
R4: (F1 ^ F2) > F3
C'est par le modus ponens que l'on déduit que val(F3) = vrai
lorsque val(F1 ^ F2) = vrai, val(R4) étant vrai ... selon le
constructeur. Certaines parties du texte peuvent présenter des
informations d'une autre nature; ce ne sont pas toujours des faits
significatifs du problème considéré. Par exemple:
"il est proposé d'allumer les grands phares" est une information
complémentaire que l'on traitera à part.
La règle R4 se réécrira:
SI le démarreur ne fonctionne pas ET
grands phares faibles
ALORS problème de batterie
Exercice: Distinguer dans ce texte les autres faits,
règles et informations complémentaires (attention, "si
... alors" ne donne pas toujours lieu à une règle ...).
Logique d'ordre 0 et logique d'ordre 1
Prenons le syllogisme classique suivant:
P1: "jean est un homme"
P2: "les hommes sont mortels"
De ces deux propositions on en déduit P3: "jean est mortel".
Selon quel mécanisme peuton faire une telle
déduction ?
Ces propositions font intervenir des classes (ou ensembles), celle des
hommes et celle des créatures mortelles. De la proposition
universelle P2(X): "Si est X est un homme alors X est mortel", on en
déduit la proposition P3 à l'aide de P1, de P2(jean) et
du Modus ponens. La logique utilisée introduit donc des
variables.
Une logique sans variable est dite d'ordre 0. Une logique qui admet des
variables est dite d'ordre 1. Les systèmes experts seront
d'ordre 0 ou 1 selon qu'ils peuvent utiliser ou non des variables dans
les propositions qu'ils manipulent.
Définition et catégorisation des systèmes
experts
En reprenant la définition de Farreny [FARRENY],
légèrement complétée, on dira qu'un
système expert est une machine déductive relativement
générale exploitant une collection séparée,
sujette à évolution, d'unités de savoirfaire
concernant un domaine particulier d'expertise humaine. Son but est
d'apporter des solutions à des problèmes bien
délimités concernant le domaine en question. Un tel
programme assure aussi des fonctions complémentaires de
dialogue, d'apprentissage et d'explication de son comportement.
Il y a différents types de systèmes experts (SE). E. G.
Aillaud en a recensé cinq, qu'il a coté d'un coefficient
de difficulté allant de 1 à 5. Un SE de coefficient de
difficulté 1 est relativement facile à réaliser,
alors qu'un système de niveau 5 est encore au stade de la
recherche [AILLAUD].
- Automatisation de manuels, de procédures, de règlements, ... (13)
- Recherche d'informations pertinentes dans une grande quantité de données (domaine des SGBD déductives) (13)
- Aide à la décision, recherche opérationnelle, logistique (24)
- Recherche de solutions à des problèmes peu formalisés (langage naturel, diagnostics complexes) (15)
- Education, formation, apprentissage (15)
Organisation des systèmes à
règles de production
Un système expert est constitué de trois "composants"
principaux:
1) base de faits: c'est l'ensemble des propositions connues du
système à un moment donné. La base de faits est
une mémoire de travail. Son contenu dépend du
problème traité.
2) base de connaissances: il s'agit de la connaissance "experte"
proprement dite. Dans les systèmes (simples) que nous
considérons, cette base est constituée d'un ensemble de
règles (P>Q) qui mettent en relation des faits dans un
domaine donné.
3) moteur d'inférence: c'est le programme informatique qui
combine les faits établis et les règles pour
établir de nouveaux faits.
Le moteur d'inférence fonctionne selon le cycle
général suivant:

Le choix de la règle se fait en plusieurs étapes:
Etape 1: La sélection des règles restreint le nombre de
règles à examiner. Cette sélection dépend
de la stratégie de recherche adoptée par le moteur.
Etape 2: Le filtrage qui détermine les règles
réellement applicables.
Etape 3: Le choix d'une règle parmi les règles
applicables (résolution du conflit).
D'autres descriptions de l'organisation d'un SE et du fonctionnement du
moteur d'inférence sont faites. Ainsi l'on regroupe parfois sous
base de connaissances, base de règles et base de faits (faits
généraux). Les faits spécifiques du
problème traités constituent alors la base de travail.
Diverses conditions peuvent être utilisées pour
arrêter le moteur:
- lorsqu'il y a saturation, c'est-à-dire lorsque plus aucun nouveau fait n'est déductible
- lorsque la base contient le fait recherché, c'est-à-dire qu'une réponse est apportée au problème posé
- lorsqu'un certain nombre de cycles, fixé au préalable a été accompli ou qu'une "profondeur" de recherche a été atteinte.
Types de fonctionnement du moteur
On a déjà vu qu'un système expert pouvait
être d'ordre 0 ou d'ordre 1 (d'autres ordres 0+, 0++, 1+ ont
été introduits pour rendre compte de dispositifs
particuliers). De nombreuses autres caractéristiques
différencient les systèmes existants. Une de
cellesci est la façon d'utiliser les règles: de la
prémisse vers la conclusion (chaînage avant) ou de la
conclusion vers la prémisse (chaînage arrière).
A titre d'exemple considérons la base de connaissance
constituée de trois règles:
REGLE r1
SI animal vole ET
animal pond des oeufs
ALORS animal est un oiseau
REGLE r2
SI animal a des plumes
ALORS animal est un oiseau
REGLE r3
SI animal est un oiseau ET
animal a un long cou ET
animal a de longues pattes
ALORS animal est une autruche
Par ailleurs on suppose que la base de faits est constituée de:
F1 : animal a des plumes
F2 : animal a un long cou
F3 : animal a de longues pattes
En chaînage avant, le moteur sélectionnera et
déclenchera les règles dont les prémisses sont
satisfaites:

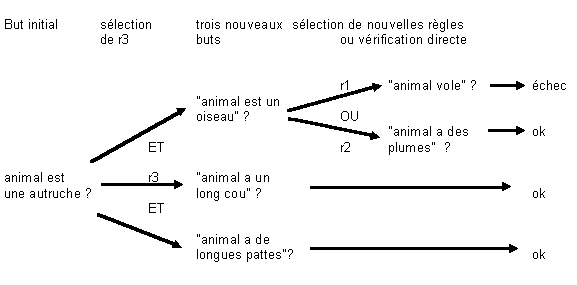
En chaînage arrière, le système part sur
un but à démontrer: par exemple F5: "animal est une
autruche". Il sélectionnera alors, de proche en proche les
règles qui permettent de prouver ce fait.
On notera par "ok" toutes les recherches qui aboutissent et par
échec les autres.
On peut décrire le fonctionnement d'un moteur en chaînage
avant ou en chaînage arrière en considérant une
seule règle, par exemple:
SI le démarreur ne fonctionne pas ET
grands phares faibles
ALORS problème de batterie
Si la conclusion est ajoutée à la base de fait
dès que la prémisse est satisfaite, c'est du
chaînage avant.
Si la conclusion n'est ajoutée à la base de fait
que lorsqu'une requête est faite à son sujet, il s'agit
alors de chaînage arrière.
Ecart entre les théories logiques et les systèmes
experts
Il y a un certain écart entre les théories logiques et
leur application dans les systèmes experts. Certaines
"accommodations" sont nécessaires. Les plus importantes
concernent l'aspect temporel, la réalisation de la valeur de
vérité et, finalement, le problème de la nature
différente de la prémisse et de la conclusion.
Aspect temporel: dans un système informatique, les
différentes opérations s'enchaînent dans le temps
alors que les principales théories logiques ne tiennent pas
compte du phénomène temporel. La distinction des
différents types de chaînage relève de cette
nécessité d'ordonner dans le temps les actions à
exécuter.
Valeur de vérité: très souvent les valeurs
de vérité ne sont pas associées
véritablement aux faits manipulés par le système.
On considère comme vrais les faits qui se trouvent dans la base
de faits. Sinon, les faits sont faux. Cette technique est connue sous
l'expression: hypothèse du monde clos. Parfois on précise
que certains faits sont inconnus (UNKNOWN).
Les faits de la prémisse (les conditions) sont simplement
testés: sontils ou non présents dans la base de
faits. Par contre, les faits de la conclusion provoquent l'ajout d'un
nouvel élément dans cette base. Ainsi une règle
dans un système expert n'est pas aussi symétrique que
l'implication logique.
SI condition 1 ET
condition 2 ET
...
condition n
ALORS action 1
action 2
...
D'autres types de conditions et d'actions seront introduites.
Structuration des faits
Afin de décrire plus facilement des familles de propositions on
considérera des faits de la forme:
nom = valeur
Par analogie avec les systèmes informatiques traditionnels, on
parlera également de variable.
Avec une telle syntaxe la règle R4 cidessus devient:
SI état_démarreur = ne_fonctionne_pas ET
g_phares = faibles
ALORS probleme = batterie
L'avantage de cette technique est de pouvoir tester toute une famille
d'hypothèses à la fois: problème = batterie,
problème = court_circuit, problème = bobine, etc. en
demandant au système de chercher la valeur de 'problème'.
Les variables, du point de vue sémantique, pourront
représenter des objets, des attributs ou d'autres choses encore,
par exemple:
* une variable peut indiquer qu'un procédé a
été utilisé:
calcul_intérêt_ok = 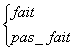
* une variable peut indiquer le procédé à utiliser
calcul_intérêt = 
* une variable peut indiquer un résultat
intérêt = 6345.65
Certaines variables seront simples, lorsqu'elles ne pourront prendre
qu'une seule valeur. Elles seront multiples si elles peuvent accepter
simultanément plusieurs valeurs.
On distingue différents types de faits:
les faitsbut: ceux qui doivent être prouvés par
le système,
les faitsquestion: ceux qui sont introduits par
l'utilisateur,
les faitssystème: qui sont internes au fonctionnement
du système.
Résumé: Un système expert (SE) est une
machine déductive, générale, exploitant une
collection d'unités de savoir-faire séparées,
sujettes à évolution, pour résoudre un
problème. Un système expert assure également les
fonctions complémentaires de dialogue, apprentissage,
explication de son comportement. Les composants de base des SE sont:
1) Base de faits: Ensemble des propositions connues du système.
C'est une mémoire de travail dont le contenu dépend du
problème traité.
2) Base de connaissance: Ensemble de règles ( P-> Q ) qui
mettent en relation des faits dans un domaine donné.
3) Moteur d'inférence: Programme qui combine les faits
établis et les règles pour établir de nouveaux
faits.