
Banca di problemi del RMT
sd120-it
 |
Banca di problemi del RMTsd120-it |
|
Individuare il fattore mancante di una moltiplicazione sapendo che è stato commesso un errore nell’applicazione dell’algoritmo e conoscendo la differenza fra il prodotto sbagliato e quello giusto.
Trovare il primo fattore di una moltiplicazione in colonna, utilizzando il numero 342 che è il secondo fattore e il numero 1836000 che è la differenza tra il risultato giusto e quello sbagliato ottenuto con un errore di incolonnamento al terzo livello.
Si può arrivare alla soluzione sia per via aritmetica che algebrica.
- Per via aritmetica (avendo più o meno consapevolezza dei fondamenti dell’algoritmo della moltiplicazione)
oppure:
una volta constatato che il prodotto parziale del terzo livello, a causa dello spostamento a sinistra, è stato moltiplicato per 10 capire che la differenza 1 836 000 è anche la differenza fra tale prodotto parziale e quello giusto (il risultato della moltiplicazione è dato dalla somma dei risultati parziali ottenuti nei vari livelli!). Fissare così l’attenzione solo sul terzo livello: abc × 3000 – abc × 300 = abc × 2700= 1 836 000 e procedere come indicato sopra.
- Per via algebrica: indicare con n il fattore incognito ed impostare un’equazione del tipo 3042n-342n = 1 836 000 oppure, impostare l’equazione 300x+40x+2x+1836000 = 40x+2x+3000x
valore posizionale, algoritmo della moltiplicazione, distributivita, equazione, primo grado
Su 1067 classi di 21 sezioni partecipanti alla prova I del 17° RMT:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 7 | 459 (86%) | 43 (8%) | 12 (2%) | 9 (2%) | 9 (2%) | 532 | 0.24 |
| Cat 8 | 307 (76%) | 40 (10%) | 12 (3%) | 18 (4%) | 25 (6%) | 402 | 0.54 |
| Cat 9 | 104 (78%) | 13 (10%) | 5 (4%) | 4 (3%) | 7 (5%) | 133 | 0.47 |
| Totale | 870 (82%) | 96 (9%) | 29 (3%) | 31 (3%) | 41 (4%) | 1067 | 0.39 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Secondo i criteri dell’analisi a priori:
- Tentativi organizzati basati sull’esecuzione sia giusta che sbagliata dell’algoritmo della moltiplicazione e sul controllo che la differenza fra i due risultati sia esattamente 1836000
- Impostazione di un’equazione di primo grado (pochissimi elaborati di cat.8, 9)
- Solo in un elaborato, fra quelli esaminati, si utilizza il fatto che la differenza fra il risultato sbagliato e quello giusto è uguale alla differenza fra il numero al terzo livello scritto con uno 0 in più (spostamento verso sinistra) e quello scritto giustamente. Poi si procede dimostrando, dapprima, che tale differenza è un multiplo di 9 e che quindi per ottenere il numero giusto del terzo livello basta fare 1836000:9 =204000. A questo punto, sapendo che il numero al terzo livello è il prodotto fra il fattore incognito e 300, per trovare il fattore incognito (680) basta fare 204000:300.
La scrittura polinomiale dei numeri e la conseguente traduzione algebrica, non sono state, in generale, utilizzate. (solo un elaborato di cat.8 scrive l’equazione 300x + 40x + 2x + 1836000 = 40x + 2x + 3000x e la risolve giustamente).
- Insufficiente padronanza dell’algoritmo della moltiplicazione
- Incapacità di impostare una ricerca organizzata
- Insufficiente padronanza dello strumento algebrico (impostazione di un’equazione con 2 incognite oppure incapacità di risolvere un’equazione correttamente impostata)
- Lettura superficiale e conseguente interpretazione sbagliata del testo:
Il problema Strana moltiplicazione pone la questione della consapevolezza degli algoritmi, gestiti per lo più in modo meccanico. Circa il 50% degli allievi ha consegnato in bianco. Risulta evidente che, pur conoscendo l’algoritmo e le proprietà della moltiplicazione, essi non sono in grado di utilizzarli in contesti diversi da quelli standard e di gestire situazioni più articolate dal punto di vista organizzativo.
Un possibile ostacolo potrebbe essere causato dal presentare l’algoritmo della moltiplicazione in modo meccanico senza riflettere sul fatto che i prodotti parziali ad ogni livello non sono niente altro che il prodotto fra il moltiplicando e, rispettivamente ad ogni successivo livello, le unità, le decine, le centinaia, . . . , del moltiplicatore. Inoltre il fatto di scrivere ad ogni livello, sotto le unità del precedente prodotto parziale, una lineetta (o il segno di uguaglianza), fa perdere di vista il significato dei prodotti parziali: sarebbe più corretto, specialmente all’inizio , aggiungere uno 0 in più ad ogni livello a partire dal secondo.
Queste considerazioni suggeriscono la necessità di condurre, fin dalla scuola primaria, attività sperimentali con gli allievi per avviarli a gestire in modo più consapevole ed autonomo sia gli algoritmi che le proprietà di tutte le operazioni. Forse potrebbe essere proprio il caso di evitare, nella scuola primaria, una conoscenza formale delle proprietà per privilegiare un approccio di tipo sperimentale che, attraverso una fase di “manipolazione” stimoli la creatività e avvii, prima di tutto, alla consapevolezza dell’utilità delle stesse.
Nella rubrica “per andare più lontano” sono riportati, a titolo di esempio, alcune attività sperimentali che il gruppo “numerazione” ha individuato e che possono essere proposte a partire dalla cat.3. Tali attività possono fornire spunti per far scoprire le proprietà “matematiche” che sono alla base degli algoritmi delle operazioni, in particolare della moltiplicazione, ed inoltre dimostrano che certe regole (es. l’incolonnamento dei prodotti parziali nella moltiplicazione o, per i più grandi, la prova del 9) non sono frutto di magia!
Sarebbe opportuno presentare agli allievi algoritmi diversi per la moltiplicazione sia per curiosità culturale sia per evidenziare quanto sia più vantaggioso l’algoritmo usuale.
Per rendere più chiaro il testo e favorire gli allievi a non incorrere in errori di cattiva interpretazione dello stesso proponiamo la seguente modifica:
Enunciato del problema modificato
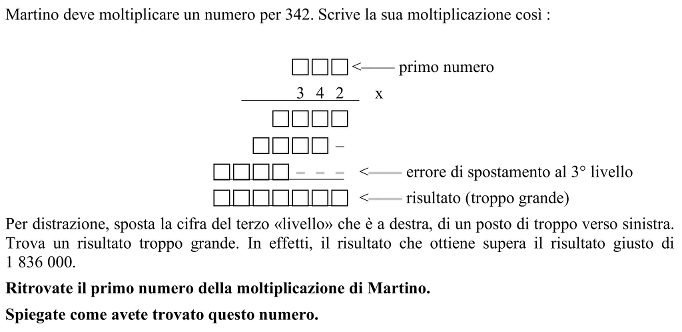
Martino deve moltiplicare un numero per 342. Scrive la sua moltiplicazione così:
[] [] [] <--- primo numero
3 4 2 x
--------
[] [] [] []
[] [] [] [] -
[] [] [] [] - - - <--- errore di spostamento al 3° livello
--------------------
[] [] [] [] [] [] [] <--- risultato (troppo grande)
Per distrazione, sposta il prodotto parziale del terzo «livello» di un posto di troppo verso sinistra. Trova un risultato troppo grande, infatti la differenza tra il risultato sbagliato e quello giusto è 1836000.
Ritrovate il primo numero della moltiplicazione di Martino.
Spiegate come avete trovato questo numero
Problemi prossimi ordinati dal più recente
Sempre 6 (I),15.F.14 (cat. 6,7,8), Sempre 6 (II),15.F.20 (cat. 9,10). Cercare se ci sono altre coppie di numeri, oltre a 7,5 e 0,8, aventi ognuno una cifra significativa (diversa da zero) dopo la virgola e il cui prodotto sia 6 Cercare quante sono le coppie di numeri decimali con due cifre dopo la virgola (la seconda significativa), il cui prodotto è 6
Una strana moltiplicazione, 26.F.14 (cat.7,8,9,10) Una strana moltiplicazione,15.F.15 (cat.7,8,9,10). Ricostruire una moltiplicazione della quale si conosce il numero delle cifre dei due fattori, tenendo presente che, nel procedere con l’algoritmo, si possono utilizzare solo le cifre 2, 3, 5, 7. Si sa , inoltre, che c’è un solo modo per sistemare le cifre.
Chifre uguali, 12.II.13 (cat.7,8). Si sa che se si moltiplica 12345679 per 0,45 si ottiene un numero che si scrive solo con nove cifre tutte uguali a 5 e una virgola. Trovare dei numeri che, quando li si moltiplica per 12345679, si scrivono solo con nove cifre tutte uguali a 7, eventualmente con la virgola.
La perdita di uno zero,15.F.13 (cat.6,7,8) Trovare un numero di tre cifre di cui una è lo 0, sapendo che se si scrive il numero tralasciando la cifra 0 e mantenendo l’ordine delle altre, si ottiene un numero di due cifre che differisce da quello di tre cifre per 441
da completare
(c) ARMT, 2009-2025