Banca di problemi del RMT
op190-it
|
|
Banca di problemi del RMTop190-it |
|
Completare "piramidi" di mattoncini secondo la regola: "il numero di un mattoncino è la somma dei numeri dei due mattoncini su quali si appoggia".
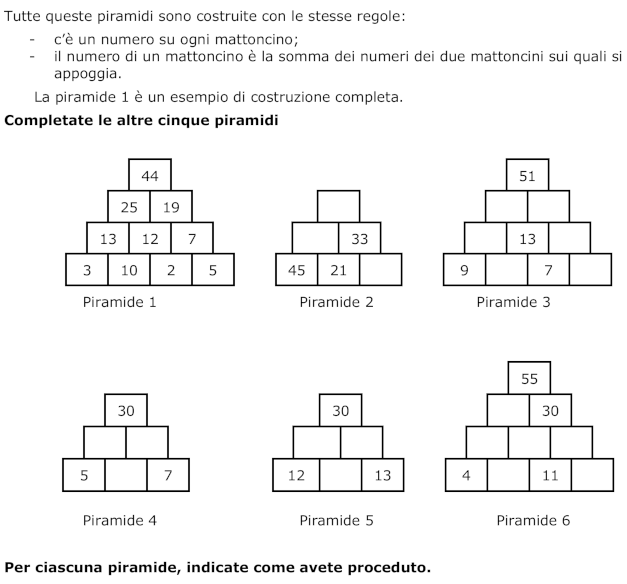
Saper completare scritture lacunari additive (equazioni), mediante addizione o sottrazione.
Secondo l'esempio della piramide 1, la piramide 2 è solo un'applicazione diretta della regola: 21 + 45 = 66; 33 + 66 = 99; 21 +... = 33, per trovare 12 in basso a destra. La Piramide 3 richiede di calcolare 6 (13 – 7 o 7 + … = 13), quindi 15 (6 + 9), quindi 28 (15 + 13), quindi 23 (51 – 28 o 28 + … = 51), quindi 10, poi 3. La Piramide 4 porta ad una “equazione” (5 + x) + (7 + x) = 30 che può essere risolta con prove successive del numero medio della base che deve essere 9 affinché la somma dei due numeri dal primo piano, ovvero 30.
La Piramide 5 è dello stesso tipo ma richiede il passaggio ad un numero innaturale perché, per prove successive: (12 + 1) + (13 + 1) = 27 troppo piccolo; (12 + 2) + (13 + 2) = 29 troppo piccolo; (12 + 3) + (13 + 2) = 29 troppo grande; bisogna provare con un numero compreso tra 2 e 3: (12 + 2,5) + (13 + 2,5) = 30!!!
La Piramide 6 combina le procedure precedenti.
addizione, sottrazione, numero naturale, numero decimale, somma, differenza
Su 9 elaborati della finale internazionale de 2024:
- Tutte e 5 le piramidi completate correttamente (7 classi)
- 3 piramidi completate correttamente (2 classi)
Considerato il successo quasi totale di questa attività, non possiamo più considerarla un problema per gli allievi di una finale internazionale, particolarmente capaci nella ricerca collettiva di soluzioni.
Quando le operazioni di addizione e sottrazione non sono direttamente applicabili, sono i tentativi che danno rapidamente la soluzione, in particolare per la piramide 5 dove il numero in basso al centro è 2,5.
Esempio: Abbiamo fatto diverse prove con le cifre e i numeri interi fino ad arrivare alla 5° piramide. Abbiamo notato che i numeri interi non funzionano, quindi abbiamo utilizzato i numeri decimali per arrivarci.
L'unica piramide non completata, da un solo gruppo, è proprio la 5a: Per noi, non può tornare.
Queste “piramidi” mettono in gioco addizioni e sottrazioni, secondo le regole della loro costruzione. Le prime tre si completano con una semplice applicazione passo passo della regola. Le tre successive richiedono dei tentativi o un’anticipazione (di tipo pre-algebrico) e questo è il loro interesse.
Nella quarta ci sono solo uno o due tentativi da fare per arrivare al “9” del mattoncino centrale in basso e non c'è bisogno di considerare una procedura più breve.
Se scegliamo numeri più grandi, una nuova strategia potrebbe rivelarsi interessante.
Ad esempio con "130" in alto e "15" e "17" alle estremità della base, il procedimento per tentativi diventa molto più lungo e incita a considerare i due mattoncini intermedi come somma di "15 e del numero ancora indeterminato della base” e “del numero ancora indeterminato della base” e “17”. Questo “numero della base” rimane provvisoriamente indeterminato ma dovrà essere contato due volte nel mattone più alto, con “15” e “17” ciascuno contati solo una volta. Entriamo così in un ragionamento prealgebrico, senza le sue scritture letterali, con un'uguaglianza lacunare.
120 = 15 + 17 + 2 x ... da completare in pochi passi con l'addizione di 15 + 17 = 32, poi il calcolo della differenza tra 32 e 120 con una sottrazione che porterà a 88 ed infine con una divisione per 2 oppure la moltiplicazione lacunare 2 x ... = 88.
Un'altra utilizzazione è il passaggio dai numeri naturali ai numeri decimali, già menzionato.
Allo stesso modo, queste piramidi potrebbero essere utilizzate per introdurre il passaggio dai numeri naturali agli interi negativi se, ad esempio, sostituissimo i due numeri 5 e 7 con 15 e 17, lasciando il numero 30 in alto.
Ci sono ancora altre utilizzazioni che lasciano diverse possibilità o un'infinità ...
Le variazioni su questo tema dei numeri disposti a piramide sono numerosissime e costituiscono tanti piccoli enigmi aritmetici.
Proposte: Dopo aver proposto il problema a tutta la classe, in gruppi e aver verificato velocemente le soluzioni, passare a nuove piramidi come quelle suggerite più sopra.
Si veda anche i problemi Pyramides (05.I.02) ; Piramidi di mattoni I (21.I.03) ; Piramidi di mattoni II (21.I.12)
(c) ARMT, -2025